Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.1 - Ex. 11
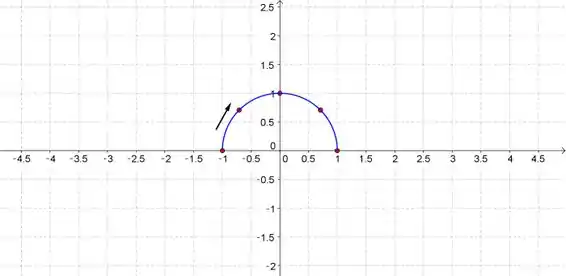
A ) Elimine os parâmetros para encontrar uma equação cartesiana da curva
B ) Esboce a curva usando as equações paramétricas para marcar os pontos. Indique com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta
Passo 1
Olá, meu amigo. Vamos resolver essa atividade.
Nos é dada a curva parametrizada:
Aqui deveremos primeiro eliminar os parâmetros e colocarmos a nossa curva parametrizada em coordenadas cartesianas. Faremos isso aproveitando da identidade trigonométrica
Já para criarmos o esboço dessa figura, iremos criar uma tabela com diferentes valores de e seus respectivos e , que são dependentes de .
Estamos já um pouco avançados agora, já pegamos alguma experiencia com os exercícios anteriores. Então bora fazer o seguinte, vamos criar uma tabela com valores de e plotar esses pontos num gráfico.
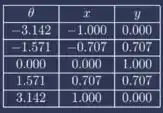
Beleza, tendo esses pontos, já podemos criar os gráficos. Antes vamos olhar nossa tabela. Percebeu que esses pontos são simétricos?
Então quando formos criar uma função ela vai acabar ficando espelhada. Outra coisa quando parametrizamos E usamos senos e cossenos. E isso é um indicativo que estamos trabalhando com funções circulares. Show? Vamos plotar nossos pontos e criar o gráfico.
Passo 2
Agora vamos voltar do mundo paramétrico para o cartesiano. Vamos cair dentro então:
Aqui vamos precisar usar um truque. Vamos ter que usar uma identidade trigonométrica
Isso vale para qualquer que seja o ângulo, inclusive , então podemos dizer que
Bem, terminamos por aqui. Esses exercícios estão no início bem intuitivos, com o tempo vamos aprender mais ferramentas para construir gráficos. Te vejo na próxima resolução :)
Passo 3
Plotando os pontos que encontramos no GeoGebra, e criando nosso gr��fico:
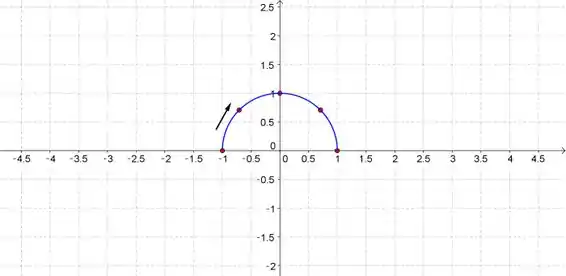
Viu só? Construímos um semicírculo. Agora só precisamos orientar. Conforme aumenta, vai de a .
Então o sentido é horário. Uma dica importante. Isso você vai pegar a pratica com o tempo, mas posso te dar esse spoiler. Rsrs
Sempre que estivermos com
Nossa função é circular e horaria. Além disso começamos a desenhar com em . Agora quando temos:
Nossa função é circular, anti-horária. E começamos a desenhar com em .
