Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 2.4 - Ex. 8
Para o limite:
Ilustre a Definição encontrando os valores de que correspondam a e .
Passo 1
O enunciado nos da :
E pede pra a gente ilustrar a definição a encontrando os valores de que correspondam a e .
Lembrando que a definição 2 diz que:
Seja uma função definida sobre algum intervalo aberto que contém o número , exceto possivelmente no próprio . Então dizemos que o limite de quando tende a é , e escrevemos:
Se para todo o número houver um número tal que se então .
Para , a definição de um limite requer que ache um tal que
O que implica em:
se
Passo 2
Se plotarmos o gráfico de , e , vamos achar que:
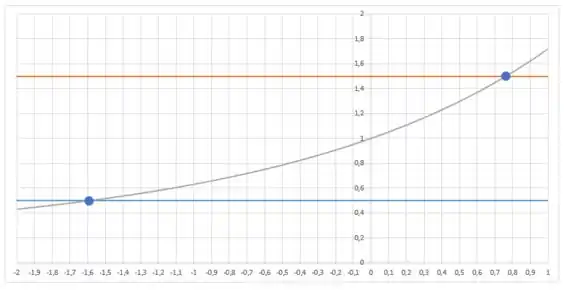
Passo 3
Vemos que a distância até a extremidade esquerda é , e a distância até a extremidade direita é .
Podemos escolher como o menor desses números, isto é . Embora tenhamos escolhido , qualquer valor menor positivo de também funcionaria.
Passo 4
Para , a definição de um limite requer que ache um tal que
O que implica em:
se
Passo 5
Se plotarmos o gráfico de , e , vamos achar que:
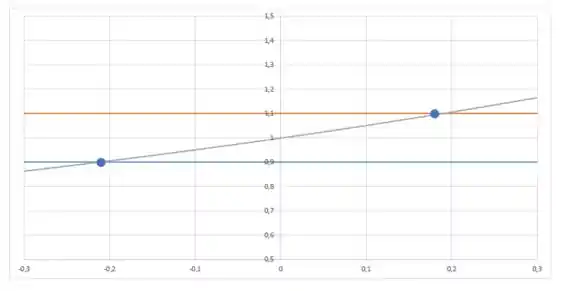
Passo 6
Vemos que a distância até a extremidade esquerda é , e a distância até a extremidade direita é .
Podemos escolher como o menor desses números, isto é .
Resposta
Desenvolvimento acima.