As linhas de escoamento (ou linhas de corrente) de um campo vetorial são as trajetórias seguidas por uma partícula cujo campo de velocidade é um campo vetorial dado. Assim, os vetores do campo vetorial são tangentes a suas linhas de escoamento.
- Use um esboço do campo vetorial para desenhar algumas linhas de escoamento. Desses seus esboços é possível descobrir qual é a equação das linhas de escoamento?
- Se as equações paramétricas de uma linha de escoamento são explique por que essas funções satisfazem as equações diferenciais e . Resolva então as equações de forma a obter uma equação da linha de escoamento que passe pelo ponto .
Passo 1
Faaaaala minha turma, tudo bem?
Essa questão tem bastante informação, então vamos sintetizar o que devemos fazer.
No item (a) devemos usar um esboço do campo vetorial para desenhar algumas linhas de escoamento, e com base nisso é possível descobrir qual a equação das linhas de escoamento.
No item (b), sabendo que as equações paramétricas de uma linha de escoamento é:
Então, devemos explicar porque essas funções satisfazem as equações diferenciais e .
Depois, resolva então as equações de forma a obter uma equação da linha de escoamento que passe pelo ponto .
Bastante informação né pessoal!? Vamos com calma.
Para resolver o item (a) vamos precisar avaliar cada quadrante, e assumir valores dentro do quadrante para entender a direção do vetor. Sabendo a direção do campo de vetores, sabemos a direção da linha de escoamento, e a partir da linha de escoamento podemos estimar uma equação.
Já no item (b), porque que as equações satisfazem? É porque um vetor velocidade nas linhas de escoamento coincide com o vetor de campo vetorial. Quando você analisa o esboço do item (a) fica claro isso.
Você precisar resolver as equações diferenciais:
Depois que resolver essas equações, uma dica para eliminar o termo t e achar uma expressão que dependa apenas de e , é você fazer vezes . Você vai perceber que vai dar igual a uma constante, e para achar o valor dessa constante aplique o ponto dado de:
Bora lá!!! Faça com calma esse exercício!
Passo 2
Vamos começar pelo item (a).
Temos a seguinte função do campo vetorial:
Vamos avaliar seu comportamento em cada quadrante. Lembre-se que:
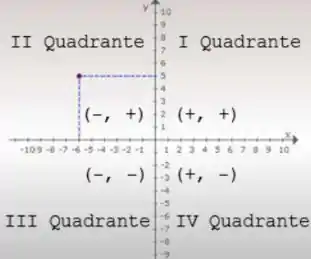
Para o primeiro quadrante, vamos pegar os pontos:
Aplicando em , temos:
Observe que o vetor está direcionado para o eixo negativo de y e para o eixo positivo de x, e conforme se afastamos da origem o tamanho do vetor aumenta.
Para o segundo quadrante, vamos pegar os pontos:
Aplicando em , temos:
Agora o vetor está direcionado para o eixo negativo de y e para o eixo negativo de x, e conforme se afastamos da origem o tamanho do vetor aumenta.
Para o terceiro quadrante, vamos pegar os pontos:
Aplicando em , temos:
Perceba, que o vetor está direcionado para o eixo positivo de y e para o eixo negativo de x, e conforme se afastamos da origem o tamanho do vetor aumenta.
Por fim, o quarto quadrante, vamos pegar os pontos:
Aplicando em , temos:
Perceba, que o vetor está direcionado para o eixo positivo de y e para o eixo positivo de x, e conforme se afastamos da origem o tamanho do vetor aumenta.
Passo 3
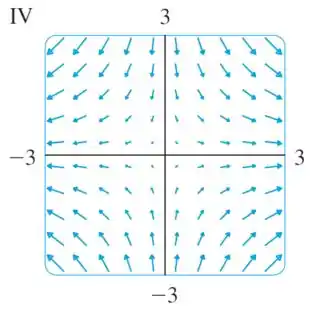
Então, já sabemos o comportamento do vetor em cada quadrante.
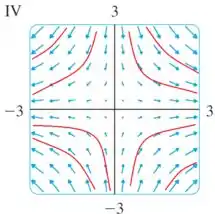
Dessa forma, podemos fazer o seguinte esboço para esse campo vetorial :
Para as linhas de escoamento, elas seguem o sentido do vetor. Observe na figura abaixo as linhas em vermelho, elas são as linhas de escoamento.
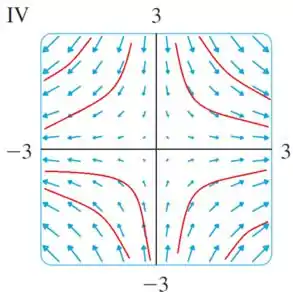
Essas linhas de escoamento tem a cara de uma função muito conhecida. A função:
Repare o gráfico dessa função:
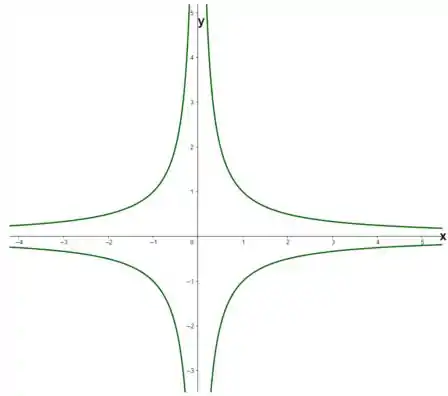
Bom, parece que as linhas de escoamento são similares aos gráficos de .
Então talvez a equação das linhas de escoamento seja .
Passo 4
Agora vamos para o item (b).
Para justificar porque as equações paramétricas de uma linha de escoamento satisfazem as equações diferenciais. Observe o seguinte:
O vetor velocidade de um ponto na linha de escoamento vai coincidir justamente com o vetor no ponto do campo vetorial.
Agora vamos focar em resolver as equações diferenciais:
Faz uma pausa, e entenda de onde saiu essas relações de equação diferencial.
A velocidade de uma partícula é dada pela derivada de sua posição em relação ao tempo:
Onde,
Logo:
Para que a trajetória siga o campo vetorial, a velocidade da partícula deve ser igual à força (ou velocidade) dada pelo campo vetorial em cada ponto. Portanto:
Logo, tem-se:
Vamos começar por . Vamos isolar e integrar ambos os lados:
Integrando, temos:
Vamos utilizar uma propriedade que envolve o logaritmo natural e exponencial, que é:
Aplicando, ficamos com:
O mesmo processo deve ser feito para . Isolando temos:
Integrando, temos:
Aplicando a propriedade da exponencial:
Ficamos com duas expressões:
Passo 5
Agora vamos tentar resolver essas equações.
Vamos fazer uma manobra para eliminar a variável . Que tal a gente fazer vezes ?! Olha só como fica:
Uma constante vezes uma constante , vai dar outra constante que vamos chamar de . Já o termo sabemos que é .
Pra determinar essa constante , basta usar o fato de que a linha de escoamento passa por :
Então, chegamos à equação:
Resposta
(a) 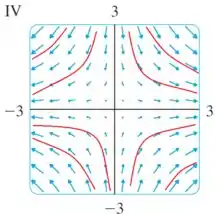
(b)