Enunciado
Cálculo - Gelson Iezzi - Fundamentos de Matemática Elementar- Ed: 9º - Capítulo 4.Exercícios - Ex. 85
Localize os arcos relacionados abaixo e, em seguida, dê o sinal da cossecante de cada um deles.
Passo 1
Fala galera, beleza? Vamos resolver mais um exercício, vem comigo!
Primeiro vamos localizar os arcos no ciclo trigonométrico
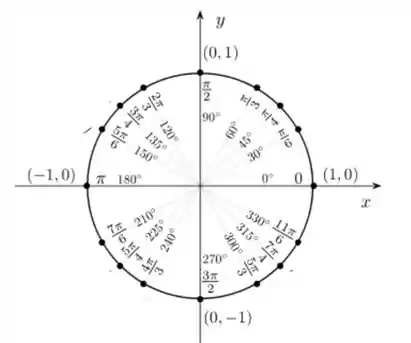
Passo 2
Agora, vamos expor algumas coisinhas sobre a função cossecante.
A função cossecante é positiva no primeiro e no segundo quadrante, e negativa nos demais.
Assim:
a) Positiva
b) Positiva
c) Negativa
d) Positiva
e) Negativa
f) Negativa
g) Negativa
h) Negativa
Resposta
a) Positiva
b) Positiva
c) Negativa
d) Positiva
e) Negativa
f) Negativa
g) Negativa
h) Negativa
Exercícios de Livros Relacionados
Calcule sen B, tg B e cotg B, sendo dado:cos B = (1)/(2) cos B = (2)/(5) cos B = 0,96 cos B = 0,17
Sabendo que B e C são complementares, calcule sen C, tg C e cotg C, quando: sen B = 0,34 sen B = 4 5 sen B = 2 3 sen B = 0,9
No ∆ ABC retângulo em A, B = 35° e c = 4 cm. Quais são os valores de a e b?
Calcule cosseno, tangente e cotangente do ângulo B, quando: s e nB = 3 5 s e n B = 2 3 s e nB = 0,57 s e nB =0,95
Sabendo que B e C são complementares, calcule cos C, tg C e cotg C, quando: cos B = 0 , 57 cos B = 5 6 cos B = 3 5 cos B = 0 , 7