Suponha que uma partícula em movimento retilíneo parta do repouso e tenha uma velocidade média de ao longo do intervalo de tempo . Esboce uma curva velocidade versus tempo para a partícula, supondo que a partícula também está em repouso no instante . Explique por que sua curva satisfaz as propriedades solicitadas.
Passo 1
Um esboço de curva que ilustra a nossa situação seria:
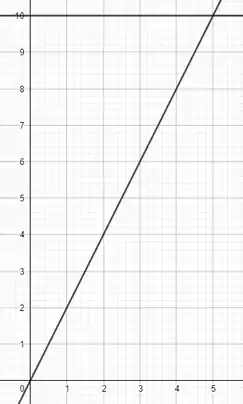
Percebemos aqui que a relação da velocidade média, , calculada é exatamente igual a 2. Temos:
Passo 2
Além disso, a curva , que cruza a curva que representa a velocidade, , exatamente no ponto . Nesse ponto, a partícula retorna ao repouso, e não mais se altera em velocidade.
Assim, passando a assumir a característica de uma função constante.
Resposta
Ei, a resposta está no passo a passo :)