Uma luz de rua é colocada no topo de um poste de 5 metros de altura. Um homem com m de altura anda afastando-se do poste com velocidade de m/s ao longo de uma reta. Com que velocidade se move a ponta de sua sombra quando ele está a m do poste?
(a) Quais são as quantidades dadas no problema?
(b) Qual é a incógnita?
(c) Faça um desenho da situação para qualquer instante .
(d) Escreva uma equação que relacione as quantidades.
(e) Termine a resolução do problema.
Passo 1
Opaa, fala ae! Beleza?? Bora resolver esse problema!
Um homem com m de altura tá andando em linha reta a m/s se afastando de um poste com de altura. Ou seja:
A medida que o homem vai se afastando do poste a sua sombra também se afasta.
a que velocidade a sombra se afasta quando ele esta a do poste, ou seja:
Mas não é só isso, temos vários itens pra responder que vão nos ajudar a chegar na resposta final! Bora lá?!
Passo 2
Item a - Os dados que o problema nos dá:
Isso daqui a gente já respondeu ali em cima! Temos
- A altura do poste ();
- A altura do homem ();
- A velocidade com que o homem se distancia do poste em um eixo que é
Passo 3
Item b: O que que o problema tá pedindo:
Também respondemos isso no Passo 1! A incógnita é a taxa de variação da posição da sombra, ou seja, .
Passo 4
Item c -Vamos fazer um esqueminha do problema:
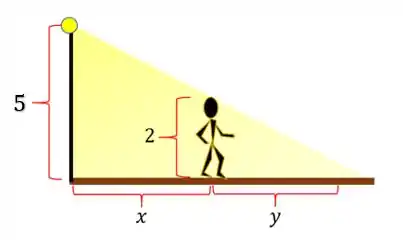
Passo 5
Item d: Esse item pede pra gente relacionar nossas variáveis.
Para relacionar e podemos usar semelhança de triângulos:
Passo 6
Item e: Agora a gente finaliza a questão!
Gente, temos que achar a velocidade da ponta da sombra quando , certo? Então, primeiro, vamos entender o quanto a sombra anda em relação ao poste.
Em relação ao poste, temos que a distância da ponta da sombra é , certo? Então, para achar a velocidade, temos que derivar a distância da sombra, ou seja:
Como vimos no passo anterior: . Assim:
Lembrando que queremos essa derivada quando . Então, derivando:
Opa, o enunciado nos dá que . Com isso:
Prontinho!! Só isso! Essa é a velocidade da ponta da sombra.
Resposta
A ponta da sombra do homem tem velocidade de