Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.9 - Ex. 19

Um homem começa a andar para o norte a m/s a partir de um ponto . Cinco minutos depois uma mulher começa a andar para o sul a m/s de um ponto a a leste de. A que taxa as pessoas estão se distanciando minutos depois de a mulher começar a andar?

Passo 1

Fala, galera! Beleza? Vamos resolver essa questão!

O enunciado pediu pra gente encontrar a taxa na qual as duas pessoas estão se distanciando, sabendo que um homem caminha para o norte a a partir de um ponto e que cinco minutos depois, a mulher caminha para o sul a , de um ponto a a leste de .

Para entender melhor o que o problema ta dizendo, vamos desenhar um esqueminha:

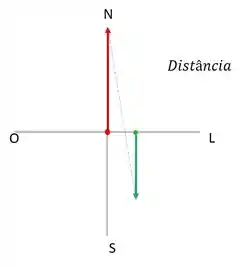
Vamos combinar uma coisa, e são positivos e e são negativos, beleza?! Além disso, como o homem anda para o norte a a partir do ponto , podemos escrever a posição do homem da seguinte forma:

A mulher anda para o sul, a a partir do ponto , mas ela só começa a caminhar min depois do homem, então podemos escrever:

Com essas coordenadas, conseguimos calcular a distância entre os dois pontos, obtendo uma expressão para a distância em função do tempo . Então, vamos derivar essa expressão para encontrar a taxa na qual os dois estão de distanciando.

Vamos lá!

Passo 2

A distância do homem à mulher é sempre o módulo da diferença entre suas posições, ou seja:

Substituindo as coordenadas que vimos no passo , temos:

Podemos cortar o :

Abrindo :

Agora vamos subtrair:

Chegamos nisso aqui:

Passo 3

Agora aplicando o teorema de Pitágoras, temos que a distância entre esses pontos pode ser dada por:

Chegamos em:

Ou, elevando ambos os lados ao quadrado:

Passo 4

Queremos a taxa na qual os dois estão se distanciando minutos depois da mulher começar a andar, então precisamos derivar a distância em relação ao tempo. Mas nesse caso a melhor forma de fazer isso é usando derivação implícita!

Então bora lá!

Calculando:

Isolando , temos:

Mas, vimos no passo anterior que:

Então, substituindo em , teremos:

Passo 5

Só que o problema quer saber quanto é essa taxa minutos depois de a mulher começar a andar , mas ela começa a andar minutos depois do homem, logo temos que considerar minutos!