Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.9 - Ex. 17

Dois carros iniciam o movimento partindo de um mesmo ponto. Um viaja para o sul a 30 k m / h e o outro para oeste a 72 k m / h . A que taxa está crescendo a distância entre os carros duas horas depois?

Passo 1

Opa, bora resolver esse problema! Temos dois carros que saem do mesmo lugar e vão pra direções diferentes. O carro A vai para o sul em uma velocidade 30 k m / h e o carro B vai pra oeste a 72   k m / h .

Aí a pergunta que a gente tem que responder é: A que taxa está crescendo a distância entre os carros duas horas depois?

Antes de qualquer coisa vamos tentar enxergar o que ta se passando, olha só:

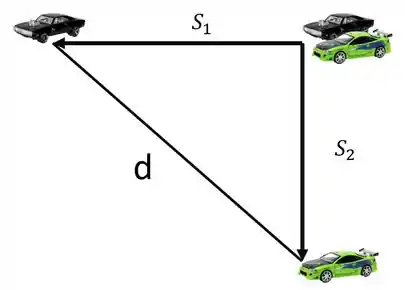
Perceba então que o que a gente quer é o quanto aquela distância d está aumentando, ou seja:

d ( d ) d t = ?

Então a gente tem que buscar um jeito de expressar esse cara; qual a primeira coisa que vêm a sua cabeça??

Claaarroo o tio Pitágoras; taca-lhe pau nesse carrinho então:

d 2 = S 1 2 + S 2 2

Passo 2

O que estamos buscando é:

d d d t

Bora derivar isso daí então:

d 2 = S 1 2 + S 2 2

Derivando dos dois lados, encontramos:

d d 2 d t = d S 1 2 d t + d S 2 2 d t

Por partes, primeiro a gente trata da potência:

2 d d d d t =   2 S 1 d S 1 d t + 2 S 2 d S 2 d t  

Simplificando tudo por 2:

d d d d t =   S 1 d S 1 d t + S 2 d S 2 d t  

Passando o d para o outro lado, ficamos com:

d d d t = 1 d S 1 d S 1 d t + S 2 d S 2 d t

Ta comigo??

Passo 3

Ou seja, no final das contas:

d d d t = 1 d S 1 d S 1 d t + S 2 d S 2 d t

Onde d S 1 d t = 30 k m / h e d s 2 d t = 72 k m / h

E após duas horas:

S 1 = 30 k m h 2 h = 60 k m         e   S 2 = 72 k m h 2 h = 144 k m

A distância d é dada por:

d 2 = S 1 2 + S 2 2

Substituindo os valores das distâncias percorridas S 1 e S 2 :

d 2 = 60 2 + 144 2

d =   60 2 + 144 2

d = 24336  

Chegamos a distância d percorrida após duas horas:

d = 156 k m

Agora vamos substituir todos os valores na fórmula:

d d d t = 1 156 60   .   30 + 144   .   72

Realizando as multiplicações:

d d d t = 1 156 1800 + 10368

d d d t = 1 156 12168

Enfim chegamos no resultado final:

d d d t = 78 k m / h

Prontinho!

Resposta

Concluindo, a distância entre os carros está variando a uma taxa de 78 k m / h , duas horas após eles se separarem.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um cocho de água tem 10m de comprimento e uma secção transversal com a forma de um trapezoide isósceles com 30c m de comprimento na base, 80c m de extensão no topo e50c m de altura. Se o cocho for pre
Uma piscina tem 5m de largura por 10m de comprimento, 1m de profundidade na parte rasa e 3m na parte mais funda. Sua secção transversal está mostrada na figura. Se a piscina for enchida a uma taxa de
Uma esteira transportadora está descarregando cascalho de 3 m 3 / m i n , constituindo uma pilha na forma de cone com o diâmetro da base e altura sempre igual. Quão rápido cresce a altura da pilha qua
Quão rápido estará o ângulo entre o chão e a escada variando no Exemplo 2 quando a parte de baixo da escada estiver a 3m da parede?
Se dois resistores com resistências R 1 e R 2 estão conectados em paralelo, como na figura, então a resistência total R , medida em ohms ( Ω ) , é dada por: 1 R = 1 R 1 + 1 R 2 Se R 1 e R 2 estão cres