Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.4 - Ex. 74
Em de maio de o ônibus espacial Endeavour foi lançado na missão STS-, cujo propósito era instalar uma peça nova em um satélite de comunicação do INTELSAT. A tabela dá os dados da velocidade para o ônibus entre o lançamento e a entrada em ação dos foguetes auxiliares.
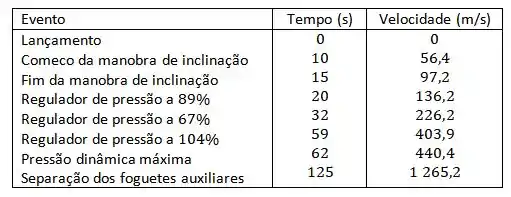
- Use uma calculadora gráfica ou computador para modelar esses dados por um polinômio de terceiro grau.
- Use o modelo da parte (a) para estimar a altura atingida pela Endeavour segundos depois do lançamento.
Passo 1
E aí, galerinha!
Nesse problema foi dada uma tabela que nos dá a velocidade de um ônibus espacial em instantes de tempo em .
A partir desses valores queremos determinar o gráfico da velocidade em função do tempo e também queremos estimar a altura atingida depois de depois do lançamento.
Parece complicado?
Para o item a) foi dito para usarmos uma calculadora gráfica, então não tem muito segredo.
Já no item b), para determinar a altura em em , temos que lembrar que a função distância é dada pela integral da função velocidade.
veja só!
Passo 2
Usando uma calculadora gráfica, vamos unir todas as funções retas que temos com as velocidades constantes que foram dadas nos intervalos de tempo. De forma, que vamos obter uma função mais ou menos com essa cara daqui.
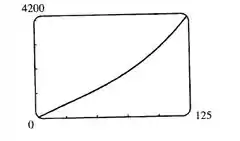
Interpolando ela a partir de uma função de terceiro grau, obtemos:
Show?
Passo 3
Para estimar a altura atingida pela Endeavour segundos depois do lançamento utilizamos o Teorema da Variação Total:
A altura no tempo é metros, afinal ele sai do chão, portanto teremos:
Vamos então calcular a integral:
Como a integral da soma é igual a soma das integrais, então
Vamos agora calcular a integral indefinida e depois utilizamos o Teorema Fundamental do Cálculo para aplicar os limites de integração:
Agora é fácil achar as primitivas de cada função, usando três expressões da Tabela de Integrais Indefinidas.
A constante pode sair da integral:
A integral da potência de é dada por:
A integral da constante é:
Bora lá!
Passo 4
Agora é só aplicar, vamos resolver elas separadamente, assim fica mais simples de ver:
Para o segundo termo...
Para o terceiro termo...
E o ultimo termo...
Agora devemos juntar tudo e usar o Teorema da Variação Total que nos diz que:
Ficamos então com:
Pronto, a estimativa da altura atingida pela Endeavour segundos depois do lançamento é de metros.
E aí! o que achou? Responde Aí!
Resposta
- A estimativa da altura atingida pela Endeavour segundos depois do lançamento é de metros.