Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.7 - Ex. 17

A massa de parte de uma barra de metal que está situada entre o extremo esquerdo e um ponto x metro a direita é 3 x 2   k g . Encontre a densidade linear (veja o exemplo 2) quando x for (a) 1m, (b) 2m e (c) 3m. Onde a densidade é maior? E menor?

Passo 1

Vamos lá! Temos uma barra de metal na seguinte situação:

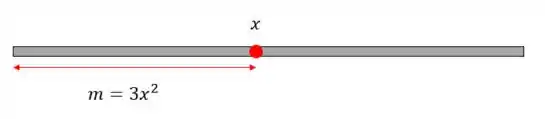
Onde m é a massa que o comprimento x dessa barra. Queremos saber a densidade linar da barra quando x for igual a ( a )   1 m ,   ( b )   2 m   e   ( c )   3 m e depois devemos comparar esses valores!

A densidade linear é a variação de massa por comprimento. Então vamos derivar m com respeito a x :

m x = 3 x 2

ρ ( x ) = m ' x = 6 x

Passo 2

Agora, basta substituir os valores no lugar de x

  1. ρ 1 = 6 k g / m

  2. ρ 2 = 12 k g / m

ρ 3 = 18 k g / m

A maior densidade é quando x = 3 e a menor quando x = 1 . Isso faz muito sentido pois a massa é prorcional ao quadrado do comprimento, então quando a gente aumenta o comprimento aumentamos muito a massa!

Resposta

  1. ρ 1 = 6 k g / m

  2. ρ 2 = 12 k g / m

ρ 3 = 18 k g / m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um balão esférico começa a ser inflado. Encontre a taxa de crescimento da área da superfície ( S = 4 π r 2 ) em relação ao raio r quando r é (a) 1 pé (ft) , (b) 2 pés (ft) e (c) 3 pés (ft). Que conclu
O volume de uma célula esférica em crescimento é V = 4 3 π r 3 Onde r é medido em micrômetros ( 1 μ m = 10 - 6 m ) . Encontre a taxa de variação média de V em relação a r quando r varia de 5 a 8 μ m 5
Os critais de cloreto de sódio são fáceis de crescer no formato de cubo, ao se permitir uma solução de água e cloreto de sódio evaporar vagarosamente. Se V for o volume de cada cubo com comprimento de
A Lei de Gravitação de Newton diz que a intensidade F da força exercida por um corpo e massa m sobre um corpo de massa M é F = G m M r 2 Em que G é a constante gravitacional e r é a distância entre os
No exemplo 6, consideramos uma população de bactérias que dobra a cada hora. Suponha que outra população de bactérias triplique a cada hora e comece com 400 bactérias. Encontre a expressão para o núme