Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 3.7 - Ex. 5
Uma massa pesando (cerca de ) estica uma mola de (polegadas; ).
Se a massa é puxada adicionais para baixo e depois é solta, e se não há amortecimento determine a posição da massa em qualquer instante . Faça o gráfico de um função de . Encontre a frequência, o período e a amplitude do movimento.
Passo 1
Vamos inicialmente fazer algumas considerações físicas do nosso problema para formula-lo matematicamente, ok?
Temos uma massa de (unidade no SI) suspensa por uma mola de tamanho de (unidade no SI), que chamamos de posição de repouso.
Vamos puxá-la para baixo por mais e depois soltá-la. Se não há amortecimentos, temos um caso ideal onde a mola tenderia a simplemente oscilar infinitamente sem parar.
Equacionando nosso problema, temos
Segunda Lei de Newton
No caso de molas, que são consideradas formas restauradoras, temos que
Onde é a contantes da mola, e é sua posição em relação à posição de repouso.
Desta forma ficamos com
Nossa equação diferencial.
Já resolvemos anteriormente problemas assim, mas a seção também aborda essa equação diferencial e nos da como solução
Onde
Chamada de frequência natural.
Qualquer duvida com relação a isso, olhar as Eq. (12) e (13).
Outra coisa que estamos interessados é no período definido como
E uma vez que, conseguimos escrever nossa função como
será a nossa amplitude.
Agora que tudo foi explicado, podemos começar nosso problema, certo?
Passo 2
Uma teoria “grande”, mas perceba que esse problema será rápido.
Primeiro observe a condição inicial do nosso problema
Onde
Onde
Assim temos que a nossa frequência será
Nosso período é dado como já mencionado, por
E por fim, temos a nossa amplitude, que perceba, é mais simples do que parece. Se puxamos a massa-mola em , então se não há amortecimentos, nossa amplitude será de
Asisim vamos escrever nosso como
Passo 3
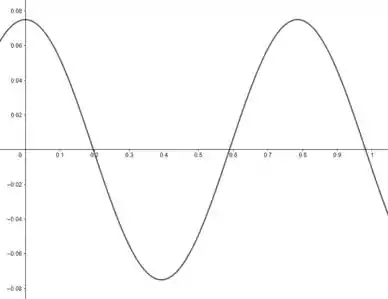
O gráfico solicitado pode ser visto a baixo
Resposta
e R