Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 3.7 - Ex. 28b
A posição de um determinado sistema mola-massa satisfaz o problema de valor inicial.
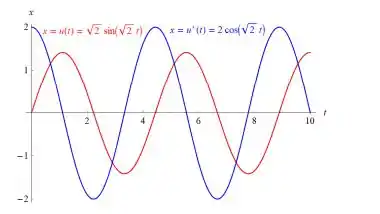
Faça os gráficos de s e de s′ em função de t no mesmo par de eixos.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para encontrarmos a solução da nossa equação. Parece muita coisa, mas é tranquilo. Partiu??
Passo 2
Ok, nosso primeiro passo vai ser relembrar que temos a seguinte relação:
A amplitude do sistema é dada por:
Usando o princípio da superposição, teremos uma combinação para tera seguinte solução geral:
Passo 3
Pronto!! Agora é só substituir os valores e achar a solução!!
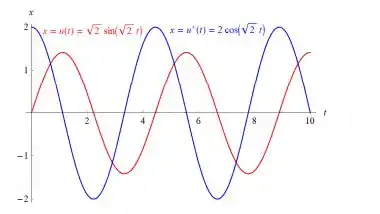
Resposta
Exercícios de Livros Relacionados
Uma massa de 100 g estica uma mola de 5c m . Se a massa for colocada em movimento a partir de sua posição de equilíbrio com uma velocidade apontando para baixo de 10c m / s , e se não houver amortecim
Uma massa pesando 2l b (cerca de 900 g ) estica uma mola de 6i n (polegadas; 6i n ≈ 15c m ).Se a massa é puxada 3i n adicionais para baixo e depois é solta, e se não há amortecimento determine a posiç
Uma massa pesando 3l b( ≈ 1,36 k g ) estica uma mola de 3i n≈ 7,6c m . Se a massa for empurrada pra cima, contraindo a mola de 1i n , e depois for colocada em movimento com uma velocidade para baixo d
Expresse a solução para o Problema 3 na forma de função cosseno dada no problema 26.
Um certo peso distende uma mola em 1 3 m e uma outra mola em 0,5m . As duas molas são atadas a um suporte rígido comum da mesma maneira que no problema 23 e na figura 5.7. O peso é então substituído p