Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 7.4 - Ex. 57

O matemático alemão Karl Weierstrass (1815-1897) observou que a substituição t =   t g x 2 converte qualquer função racional de s e n   x e c o s   x em uma função racional ordinária de t.

  1. Se t =   t g x 2 ,   - π < x < π , esboce um triângulo retângulo ou use as identidades trigonométricas para mostrar que:

    2. c o s x 2 = 1 1 - t ²           e         s e n x 2 = t 1 - t ²

  2. Mostre que:

    3. c o s x = 1 - t ² 1 + t ²           e         s e n x = 2 t 1 + t ²

  3. Mostre que:

d x = 2 1 + t ² . d t

Passo 1

Bom galera, antes de começar vamos lembrar que:

t g x 2 = C a t e t o   O p o s t o C a t e t o   A d j a c e n t e

Se:

t g x 2 = t

Então:

t g x 2 = C a t e t o   O p o s t o C a t e t o   A d j a c e n t e = t 1

Ou seja, já temos as medidas dos dois catetos. Agora só precisamos achar a hipotenusa.

Já sabem como se calcula né?

h i p o t e n u s a ² = C O ² + C A ²

h i p o t e n u s a ² = t ² + 1

h i p o t e n u s a = t ² + 1

Desenhando o triângulo:

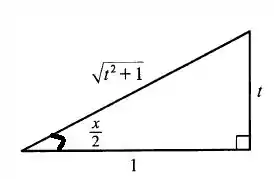
Para finalizar a letra a precisamos do seno e do cosseno.

O seno é dado por:

s e n   x 2 = C O H = t t ² + 1

E

cos ⁡ x 2 = C A H = 1 t ² + 1

Passo 2

Para a letra b precisamos lembrar que:

cos ⁡ ( x ) = cos ⁡ 2 . x 2

Se lembrarmos da identidade:

cos ⁡ ( 2 x ) = 2 . c o s ²   x - 1

Adaptando:

cos ⁡ 2 . x 2 = 2 . c o s ²   x 2 - 1

Já sabemos o cosseno, então vamos substituir:

cos ⁡ ( x ) = 2 . 1 t 2 + 1 2 - 1

cos ⁡ ( x ) = 2 t 2 + 1 - 1 = 2 - t 2 - 1 t 2 + 1 = 1 - t 2 t 2 + 1

Para o seno também podemos:

sen ⁡ ( x ) = sen ⁡ 2 . x 2

Usando a identidade:

s e n   2 x = 2 . s e n   x . cos ⁡ x

Adaptando:

s e n   2 . x 2 = 2 . s e n   x 2 . cos ⁡ x 2

Substituindo:

sen ⁡ ( x ) = 2 . t t 2 + 1 . 1 t 2 + 1 = 2 t t 2 + 1

Passo 3

Para achar a derivada de x, antes nós temos que isolá-lo. Se usarmos:

t g x 2 = t

Quando fazemos o arco tangente:

x 2 = t g - 1 t

x = 2 . t g - 1 t  

Lembrando que a derivada de t g - 1 t é 1 1 + t ² . Podemos derivar x:

d x = 2 . 1 1 + t ² . d t

Então:

d x = 2 1 + t ² . d t

E finalizamos mais umaa!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na figura, o comprimento da corda A B é 4 cm, e o comprimento do arco A B é 5 cm. Encontre o ângulo central θ , em radianos, correto até a quarta casa decimal. Dê então a resposta com precisão de um g
Demonstre a fórmula para d d x cos - 1 ⁡ x pelo mesmo método usado para d d x sin - 1 ⁡ x .
a Uma maneira de definir s e c - 1 x é dizer que y = s e c - 1 x ↔ sec ⁡ y = x e 0 ≤ y ≤ π ou π ≤ y ≤ 3 π 2 . Mostre que, se essa definição for adotada, então d d x s e c - 1 x = 1 x x 2 - 1 ( b ) Out
Derive cada identidade trigonométrica para obter uma nova identidade (ou uma familiar).
Calcule f ' x sendoa) f x = tg ⁡ x b) f x = sec ⁡ x