Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.4 - Ex. 59a

O matemático alemão Karl Weierstrass (1815-1897) observou que a substituição t = t g x 2 converte qualquer função racional de s e n   x e cos ⁡ x em uma função racional ordinária de t .

a) Se t = t g   x 2 , - π ≤ x ≤ π , esboce um triângulo retângulo ou use as identidades trigonométricas para mostrar que

cos ⁡ x 2 = 1 1 + t 2     e     s e n x 2 = t 1 + t 2

Passo 1

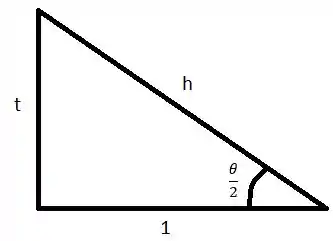
A questão forneceu a tangente de x / 2 em função de t e devemos escrever o seno e cosseno desse ângulo em função de t . Desta forma, vamos desenhar o triângulo retângulo com ângulo x / 2 , cateto oposto t , cateto adjacente 1 e hipotenusa h :

Passo 2

Primeiro vamos calcular h pelo teorema de Pitágoras:

h 2 = 1 2 + t 2 ⇒ h = 1 + t 2

Passo 3

O seno é cateto oposto sobre hipotenusa. Assim,

s e n   x 2 = t h = t 1 + t 2

Já para o cosseno:

cos ⁡ x 2 = 1 h = 1 1 + t 2

Resposta

Demonstração.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

f) ∫ t g 5 x sec 4 ⁡ ( x ) d x
d) ∫ t g 3 3 xd x
a) ∫ c o t g x d x = l n | s e n ( x ) | + c
e) ∫ c o t g n x c o s s e c ( x ) d x = - c o t g n + 1 x n + 1 + c
d) ∫ c o t g 2 x d x = - c o t g x - x + c