Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.9 - Ex. 70
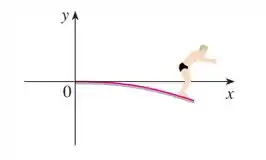
Se um mergulhador de massa permanece na ponta de um trampolim de comprimento e densidade linear , o trampolim toma a forma da curva , em que
são constantes positivas que dependem do material do trampolim e é a aceleração da gravidade.
(a) Encontre uma expressão para a forma da curva.
(b) Use para estimar a distância da horizontal à ponta do trampolim.
Passo 1
Pessoal nessa questão nos foi dado que temos a seguinte relação
E queremos encontrar a função .
Para isso vamos usar o conceito de antiderivada.
A antiderivada é uma função que quando derivamos resulta em :
E se é uma antiderivada de nesse intervalo, então a antiderivada mais geral de é:
onde é uma constante qualquer, afinal, quando derivamos a constante obtemos zero, logo somar uma constante a não muda em nada sua derivada.
Aqui vai nos ajudar saber a antiderivada da potência:
E da constante:
E também vale lembrar que a constante multiplicada a função não altera em nada sua derivada ou antiderivada:
Como a função determina a altura do trampolim com relação a horizontal, temos que
Além disso, também temos que é a variação dessa posição com a horizontal, se olharmos o desenho, vemos que na posição essa variação �� horizontal, e só depois que ela começa a ficar inclinada para baixo:
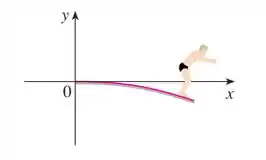
Dessa forma também poderemos dizer que
Vamos usar esses valores para encontrar as constantes que forem aparecendo no processo de antiderivação.
Passo 2
Temos que:
Podemos abrir o produto notável da direita:
Dessa forma teremos:
Vamos agora trabalhar na antiderivada.
Do lado esquerdo temos:
Do lado direito temos a antiderivada dos termos:
Juntando tudo com uma constante teremos:
Usando nossa condição que é:
Teremos:
Logo,
Passo 3
Antiderivando novamente teremos:
Do lado esquerdo:
Do lado direito:
Juntando tudo com uma nova constante teremos:
Desde que a extremidade esquerda da borda esteja fixa, nós teremos que:
quando
Então:
Consequentemente,
Dessa forma, temos:
E escrevendo para teremos:
Passo 4
, logo a extremidade da borda tem uma distância de aproximadamente abaixo da horizontal.
Pelo resultado em (a) nós calculamos:
O que resulta em:
Esse valor é positivo pois é negativo.