Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.9 - Ex. 78
Um modelo de foguete é lançado para cima a partir do repouso. Sua aceleração para os três primeiros segundos é , e nesse ínterim o combustível acaba, e ele se transforma em um corpo em queda livre. Após s o paraquedas do foguete se abre, e a velocidade (para baixo) diminui linearmente para m/s em segundos. O foguete então cai até o solo naquela taxa.
(a) Determine a função posição e a função velocidade (para todo instante ). Esboce os gráficos de e .
(b) Em que instante o foguete atingiu sua altura máxima e qual é essa altura?
(c) Em que instante o foguete atinge a terra?
Passo 1
Eaee, belezinha??
Bom... a questão nos dá um lançamento vertical de um foguete que, em seguida, cai com a ajuda de um paraquedas.
A aceleração em relação ao tempo nos três primeiros segundos é de:
Quando passa esses três segundos o combustível acaba e o corpo cai em queda livre.
Após s o paraquedas do foguete se abre, e a velocidade (para baixo) diminui linearmente para m/s em segundos... até chegar no solo.
Queremos determinar a função posição e a função velocidade (para todo instante ) e esboçar os seus gráficos.
A questão também quer que calculemos o instante em que o foguete atingiu sua altura máxima (e sua altura nesse momento).
Também queremos calcular o instante em que o foguete atinge a terra.
Bastante coisa, não é?
Nesse caso, o foguete tem três comportamentos distintos... primeiro acelera, depois cai em queda livre e por fim desacelera até cair no chão.
Então para resolver esse problema vamos analisar cada um desses intervalos separadamente.
Inicialmente temos apenas a aceleração do foguete, então para obter as funções velocidade e espaço, temos que calcular as primitivas de primeira e segunda ordem de .
Como é uma função linear, para calcular suas primitivas, vamos aplicar a regra inversa da regra da potência.
Para .
E aí?? Bora lá?? 😉
Passo 2
Para nós temos .
Como , a primitiva é:
, então:
Uma vez que , é a primitiva de , portanto:
, então:
Notamos que e .
Show?
Passo 3
Para nós temos .
Como , a primitiva é:
, então:
Uma vez que , é a primitiva de , portanto:
, então:
Notamos que e .
Tranquilo até aqui?
Passo 4
Para temos que a velocidade aumenta de para nesse período, logo:
Uma vez que , é a primitiva de , portanto:
Estamos quase no fim!
Passo 5
Para : , então:
, então:
Portanto, até o foguete atingir a terra nós temos:
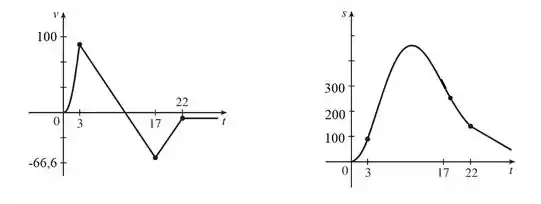
Maravilha!
Passo 6
Para encontrar a altura máxima, nós pegamos o em e igualamos a .
A altura máxima é:
Tranquilo até aqui?
Passo 7
O foguete atinge a terra quando , então:
Entendeu direitinho?? Responde Aí! 😉