Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.7 - Ex. 56
Um modelo para o rendimento de uma cultura agrícola em função do nível de nitrogênio e fósforo no solo (medido em unidades apropriadas) é
onde é uma constante positiva. Quais níveis de nitrogênio e fósforo resultam no melhor rendimento?
Passo 1
Fala aí! tudo certinho?
Neste exercício, temos uma fórmula que relaciona o rendimento de uma plantação com a quantidade de nitrogênio e fósforo que tem no solo. A fórmula é essa aqui:
O que o exercício nos pede é encontrar os valores de nitrogênio e fósforo que fazem o rendimento ser o maior possível.
Como vamos resolver isso?
O que queremos o valor de e que maximizam o valor de !
Uma forma de fazer isso é usar o método das derivadas parciais, que consiste em calcular a variação do rendimento em relação a cada variável, e igualar a zero.
Assim, podemos encontrar os pontos críticos da função, que são os candidatos a serem os máximos ou mínimos.
Depois, temos que testar esses pontos para ver se eles realmente são máximos pelo teste da segunda derivada:
Montamos a equação da matriz hessiana:
E analisamos os sinais de e .
Se e , o ponto é de mínimo, se o ponto é de máximo.
Se o ponto é sela e se não podemos afirmar nada.
Sacou! Bora começar!
Passo 2
Bom galera, vamos começar pegando as derivadas parciais:
Pela regra do produto e da cadeia, temos:
Como e tem uma simetria estrutural em , podemos calcular invertendo e ...
Beleza, Então precisamos encontrar os pontos críticos com as derivadas parciais:
Com isso podemos deduzir que: ou ou
No caso da exponencial não é possível porque para ela ser , precisa ser , e isso também faz com que .
Logo:
Do mesmo jeito em:
Então nosso ponto critico é:
Show?
Passo 3
Vamos calcular as derivadas de segunda ordem agora.
Novamente por simetria...
Calculando agora a derivada mista.
Com isso temos que o determinante da matriz hessiana é:
Perceba que é sempre positivo por causa do expoente par.
Ao mesmo tempo é negativo por causa do sinal negativo e consideranto positivo.
Então é um ponto de máximo.
O gráfico fica assim:
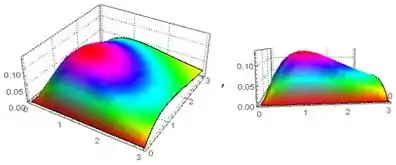
É isso! O que achou? Responde Aí!
Resposta
é o ponto máximo.