Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 16.5 - Ex. 21

Determine o paralelepípedo-retângulo de volume máximo, com arestas paralelas aos eixos, inscrito no elipsoide

x 2 4 + y 2 9 + z 2 16 = 1

Passo 1

Um enunciado mais claro para este problema seria: “Para uma caixa de lados a , b e c , maximize o volume V = a b c , devendo seus vértices pertencer ao elipsoide dado”. Aí pronto! Matamos o enunciado!

Uma representação do problema nos ajudará a desenvolver melhor a solução:

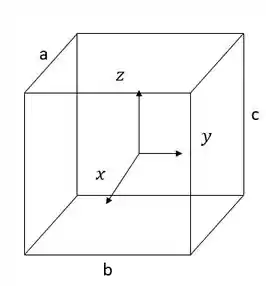
Vemos que o volume total é simplesmente dado por V = a b c .

Note que x = a / 2 ,   y = b / 2 e z = c / 2 (colocamos a caixa no centro do elipsoide!!).

Em temos de nomenclatura, neste exercício identificamos:

f = a b c  

g = a / 2 2 4 + b / 2 2 9 + c / 2 2 16 - 1

Lembrando que a f sempre vai ser a função que queremos minimizar/maximizar e g sempre representará uma restrição na forma g = 0 (no caso, os vértices da caixa devem estar tocando o elipsoide dado).

Agora, devemos resolver o sisteminha

∇ f = λ ∇ g g = 0

Para achar os pontos de máximo/mínimo.

Passo 2

Vamos começar calculando o vetor ∇ f :

∇ f = ∂ f ∂ a , ∂ f ∂ b , ∂ f ∂ c = b c , a c , a b

Ótimo! Agora façamos o mesmo para o vetor ∇ g :

∇ g = ∂ g ∂ a , ∂ g ∂ b , ∂ g ∂ c

A primeira derivada fica

∂ g ∂ a = ∂ ∂ a a / 2 2 4 = ∂ ∂ a a 2 16 = a 8

E as outras

∂ g ∂ b = b 18

∂ g ∂ c = c 32

O gradiente então fica

∇ g = a 8 , b 18 , c 32

E pronto, já temos os gradientes!

Passo 3

Agora, vamos substituir ∇ f e ∇ g no sisteminha ∇ f = λ ∇ g g = 0 , o que nos fornece:

b c , a c , a b = λ a 8 , b 18 , c 32 a / 2 2 4 + b / 2 2 9 + c / 2 2 16 - 1 = 0

Lembre-se que este sisteminha na verdade representa 4 equações:

b c = λ a 8 a c = λ b 18 a b = λ c 32     a / 2 2 4 + b / 2 2 9 + c / 2 2 16 = 1

Sisteminha complicado! Vamos dividir a primeira equação pela segunda. O resultado é

b a = a b 9 4

O que implica de imediato que b = 3 2 a .

Do mesmo modo, dividindo a terceira equação pela primeira, achamos

a c = c a 1 4

O que nos leva de imediato até c = 2 a . Ou seja, todos os lados devem ter um valor proporcional a a ! Mas, qual valor?? Basta substituir na equação que sobrou:

a / 2 2 4 + b / 2 2 9 + c / 2 2 16 = a / 2 2 4 + a / 2 2 4 + a / 2 2 4 = 3 16 a 2 = 1

Ou seja, temos a = 4 3 , e daí b = 3 2 a = 6 3 e c = 2 a = 8 3 .

Resposta

Caixa de arestas 4 3 , 6 3 e 8 3 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Entre todos os triângulos de perímetro igual a 10 cm, encontrar o que tem maior área
Em uma empresa que produz dois diferentes produtos, temos as funções de demanda: Q 1 = 40 - 2 P 1 - P 2 Q 2 = 35 - P 1 - P 2 onde Q i ,i = 1,2 , representa o nível de produção do i-nésimo produto por
Encontrar o ponto da esfera x 2 + y 2 + z 2 = 4 mais próximo do ponto (3, 3, 3).
Nos exercícios 35 a 43, determinar os valores máximo e mínimo da função dada, na região indicada.38. z = s e nx + s e ny + s e nx + y ; 0 ≤ x ≤ π e 0 ≤ y ≤ π .
Nos exercícios 35 a 43, determinar os valores máximo e mínimo da função dada, na região indicada.35. f x ,y = x + 2 y ; no retângulo de vértices 1 ,- 2 ,1 ,2 ,1 ,- 2 e - 1 ,- 2 .