Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 14.7 - Ex. 55
Suponha que um cientista tenha razões para acreditar que duas quantidades e estejam relacionadas linearmente, ou seja, , pelo menos aproximadamente, para algum valor de e de . O cientista realiza uma experiência e coleta os dados na forma de pontos e então coloca-os em um gráfico. Os pontos não estão todos alinhados, de modo que o cientista quer determinar as constantes e para que a reta “ajuste” os pontos tanto quanto possível (veja a figura).
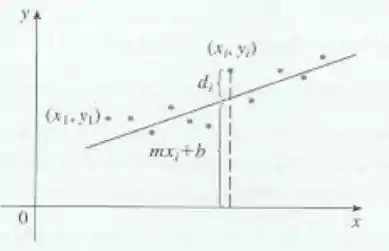
Seja o desvio vertical do ponto da reta. O método dos mínimos quadrados determina e de modo a minimizar , a soma dos quadrados dos desvios. Mostre que, de acordo com esse método, a reta de melhor ajuste é obtida quando
Assim, a reta é determinada resolvendo esse sistema linear de duas equações nas incógnitas
e . (Veja a Seção 1.2 do Volume I para mais aplicações do método dos mínimos quadrados.)
Passo 1
Note que aqui as variáveis são e , e a função que queremos minimizar é:
Mas, como , teremos:
Passo 2
Show! Agora vamos determinar a derivada parcial de em relação a e igualá-la a :
Com isso, acabamos de mostrar a segunda equação que o enunciado nos pediu.
Passo 3
Agora, para mostrar a primeira equação, vamos determinar a derivada parcial de em relação a e igualá-la a :
Resposta
Ei, a resposta está no passo a passo :)