Use o campo de direções I para esboçoar os gráficos das soluções que satisfazem as condições iniciais dadas.
a) b) c)
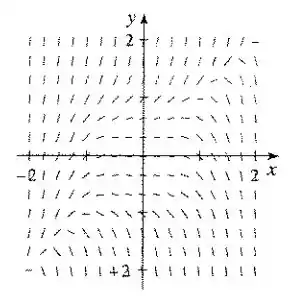
Passo 1
O exercício pede para esboçarmos sobre o campo de direções dado a curva que representa a solução da equação diferencial com diferentes condições iniciais. Para isso, basta identificar o ponto no campo e completar o desenho.
Para o item (a), temos , de modo que chegamos no ponto . Agora basta completar a curva seguindo as tangentes:
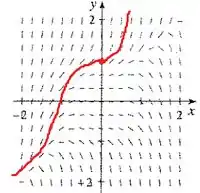
Passo 2
Já no item (b), temos , de modo que marcamos o ponto :
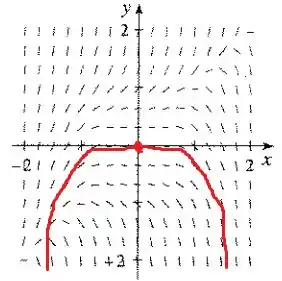
Passo 3
Por fim, no item (c), temos , de modo que o ponto de partida é :
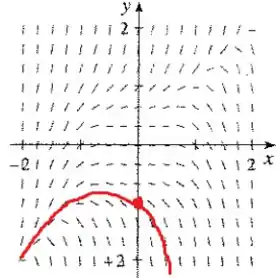
Resposta
Esboço de curvas.