Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 9.2 - Ex. 3
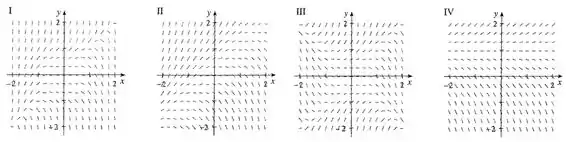
Ligue a equação diferencial a seu campo de direções (I-IV). Dê razões para sua resposta.
Passo 1
Show de bolinhas então galera bonita, a gente tá afim de encontrar o campo de direções da equação , e esse tal campo de direções é aquele campo cheio de “risquinhos” ali, onde cada risquinho representa a direção, ou melhor, a inclinação da nossa equação. E como a gente é malandro sabemos que a derivada de uma função fornece também pra gente a incliniação, ou seja, na equação , o termo “” que representa a derivada de , fornece pra gente a inclinação de , . Podemos observar que essa inclinação depende somente dos valores de , sendo então independente de . Isso quer dizer que substituindo os valores de y na equação vamos obter as inclinações dos risquinhos ao longo das retas. Então bora lá
Passo 2
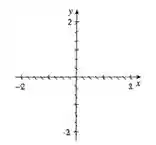
Vamos então substituir os valores de y na nossa equação que estão dentro da nossa escala, e verificar a inclinação do risquinho. Para , temos que
Logo, ao longo da reta , a inclinação dos risquinho será de , desse jeito
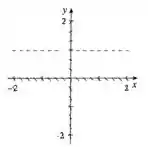
Agora para , temos que
Isso quer dizer que a inclinação dos risquinhos ao longo da reta , será igual a , ou seja, os risquinhos estarão na horizontal dessa forma
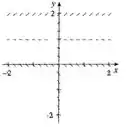
Da mesma maneira, agora para , temos que
Logo a inclinação ao longo da reta é de 45° e os risquinhos estarão dispostos de tal maneira
Passo 3
Agora que a gente tem um esboço de como tá ficando o campo de direções, a gente pode comparar com as repostas, nosso campo é esse
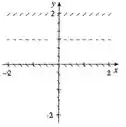
E as alternativas são essas aqui
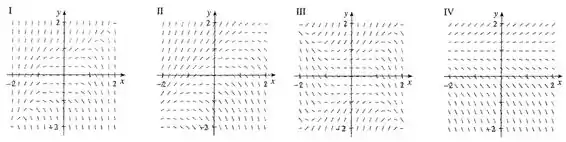
E observando bem de pertinho a gente pode ver que o campo IV é o único que se encaixa no campo que a gente encontrou. Agora ficou bonito
Resposta
IV