Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.1 - Ex. 50

Mostre que a área da elipse da figura abaixo é π a b . [Sugestão: Use uma fórmula de Geometria]

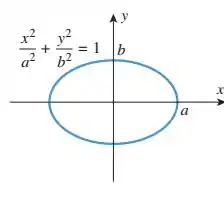
Passo 1

Para encontrar a região englobada por curvas, precisamos analisar a região dada e montar a integral:

A = ∫ a b f m a i o r - f m e n o r d x

Ou

A = ∫ c d g m a i o r - g m e n o r d y

E calculá-la. Vamos lá!

Passo 2

Como nossa região tem simetria, podemos só achar a região que está no primeiro quadrante e multiplicar por quatro. Vamos achar uma y = f ( x ) nesse quadrante a partir da equação:

x 2 a 2 + y 2 b 2 = 1 ∴ y = b 1 - x 2 a 2 = b a a 2 - x 2

A gente percebe que como temos uma função que varia em x , é melhor montarmos a integral em relação a esse eixo. Outra que coisa que vemos é que na nossa região, a função y = b a a 2 - x 2 é a maior e y = 0 é a menor. Além disso vemos também que no eixo x , a região está limitada entre 0 e a . A integral, então, fica com essa carinha:

A = 4 ∫ 0 a b a a 2 - x 2 d x

Passo 3

Agora é só calcular a integral:

A = 4 b a ∫ 0 a a 2 - x 2 d x

Fazendo a substituição trigonométrica x = a s e n ( θ ) , e resolvendo a integral:

A = 4 ⋅ 1 4 π a b

A = π a b

Resposta

Prova nos passos

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcular a área da região entre as curvas{[[x = 4 cos t],[y = 2 s e n t]]) e {[[x = cos t],[y = s e n t]])
Calcular a área entre o arco da hipociclóide x = 3 cos 3 ⁡ t y = 2s e n 3t , tϵ[ 0 , π 2 ] e a reta x + y = 3 .
Calcular a área da região limitada pelas seguintes curvas, dadas na forma paramétrica. x = 2 cos 3 ⁡ t y = 2s e n 3t e x = 2 cos ⁡ t y = 2s e nt
Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas. y = e x ,x = 0 ,x = 1ey = 0
Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas. y = 5 - x 2ey = x + 3