Faça um gráfico de diversos membros de uma família de curvas com equações paramétricas , , onde a > 0. Como muda o formato quando a aumenta? Para quais valores de a curva tem pontos de mínimo?

Quando está próximo de , é como a linha . Ela adquire partes pontiagudas à medida que começa a aumentar.

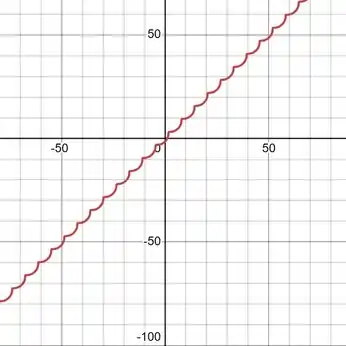
Em algum lugar entre e laços estreitos e muito pequenos começam a se formar em partes que parecem pontiagudas. (visíveis apenas se você conseguir ampliar bastante)

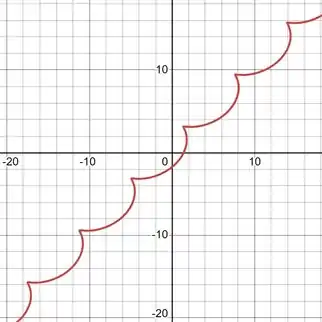
Conforme aumenta, os laços aumentam de tamanho.

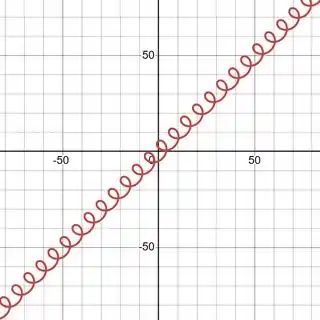
Está curva só começara a ter valores de mínimo quando os loops começarem, caso contrário ela não tem valores de mínimo. E isso começa a acontecer a partir de , mas é válido lembrar que nunca teremos um mínimo global pois o tamanho dos loops para cada valor de , se mantém os mesmos, só teremos mínimos locais.