Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.1 - Ex. 30
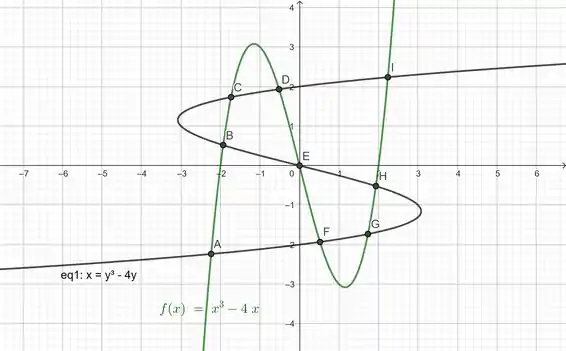
Trace as curvas e e encontre seus pontos de intersecção, com precisão de uma casa decimal.
Passo 1
Olá, meu amigo. Vamos resolver mais uma atividade?
Aqui nos são dadas as curvas:
E
Para identificarmos os pontos de intersecção entre as duas curvas, podemos desenhá-las em um memos plano cartesiano, isso nos permite identificar alguns pontos com maior facilidade.
Como essa atividade requer o uso de software grafico, vamos utilizar o GeoGebra, para nos ajudar a traçar melhor as curvas.
Passo 2
Então, com ajuda do GeoGebra, plotamos as curvas juntas, em um único plano cartesiano:
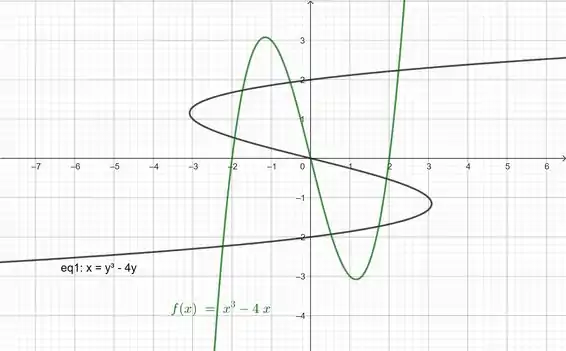
Para fazer isso, basta colocar as equações das retas no campo do lado esquerdo da tela:
O ponto é um ponto de intersecção que sabemos apenas olhando o gráfico.
Abaixo a gente vai ver a intersecção de todos os pontos:
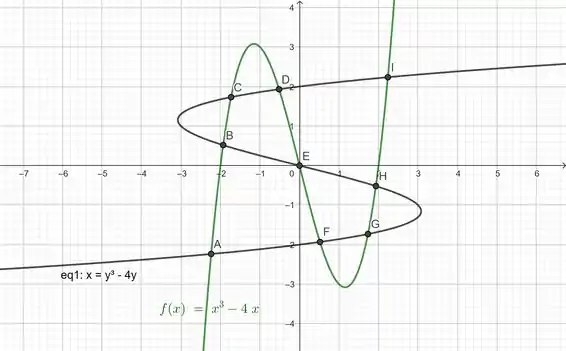
Para fazer isso de forma automática utilizando o GeoGebra, você vai fazer o seguinte:
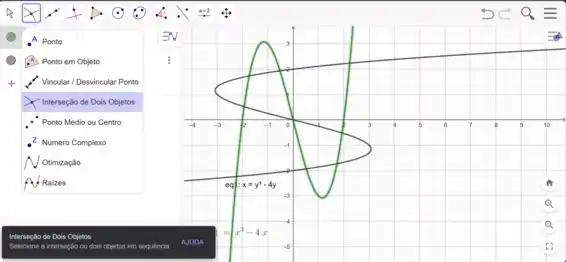
Você vai clicar na opção interseção de dois objetos, após isso é só clicar nas duas curvas e ser feliz.
No painel de equações vai aparecer os pontos e as coordenadas de todas as interseções.
Resposta
