Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.3 - Ex. 84

  1. Mostre que e x ≥ 1 + x para x ≥ 0 .
  2. Deduza que e x ≥ 1 + x + 1 2 x 2 para x ≥ 0 .
  3. Use a indução matemática para demonstrar que para x ≥ 0 e qualquer inteiro positivo n ,

e x ≥ 1 + x + x 2 2 ! +   · · · + x n n !

Passo 1

Fala queridos....

Nessa questão temos que mostrar que e x ≥ 1 + x para x ≥ 0 .

Para isso vamos usar a função

f x = e x - 1 - x

Encontrar sua derivada e provar que essa função é crescente, o que nos dará no final das contas o que queremos.

Depois vamos deduzir o mesmo para e x ≥ 1 + x + 1 2 x 2 e para isso faremos o mesmo procedimento.

Por fim vamos usar indução matemática para demonstrar que

e x ≥ 1 + x + x 2 2 ! + … + x n n !

Passo 2

Vamos fazer f x = e x - 1 - x e analisar os sinais de f ' ( x ) :

Para x ≥ 0 nós temos:

f ' ( x ) = e x - 1 - x ' = e x - 0 - x 1 - 1 = e x - 1 ≥ 0

e x = 1 → x = 0

f 0 = e 0 - 1 - 0 = 0

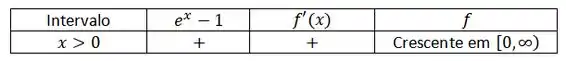
Já que f 0 = 0 e f é crescente em 0 , ∞ :

f x ≥ 0 para x ≥ 0

e x - 1 - x ≥ 0

e x ≥ 1 + x

Passo 3

Vamos fazer f x = e x - 1 - x - 1 2 x 2 e analisar os sinais de f ' ( x ) :

Para x ≥ 0 nós temos:

f ' x = e x - 1 - x - 1 2 x 2 ' = e x - 0 - x 1 - 1 - 1 2 . 2 . x 2 - 1 = e x - 1 - x

Para x ≥ 0 , nós já provamos (no Passo 1) que e x ≥ 1 + x , logo, podemos dizer que f ' x = e x - 1 - x ≥ 0 .

f 0 = e 0 - 1 - 0 - 1 2 0 2 = 0

Já que f 0 = 0 e f é crescente em 0 , ∞ :

f ( x ) ≥ 0 para x ≥ 0 → e x - 1 - x - 1 2 x 2 ≥ 0 → e x ≥ 1 + x + 1 2 x 2

Passo 4

Pela parte (a) o resultado vale para n = 1 , vamos supor que:

e x ≥ 1 + x + x 2 2 ! +   · · · + x k k ! para x ≥ 0

Fazendo:

f x = e x - 1 - x - x 2 2 ! - · · · - x k k ! - x k + 1 k + 1 !

Temos que f ' x é por suposição:

f ' x = e x - 1 - x - · · · - x k k ! ≥ 0

Consequentemente, f ( x ) é crescente em 0 , ∞ , então x ≥ 0 implica que:

0 = f ( 0 ) ≤ f x = e x - 1 - x - · · · - x k k ! - x k + 1 k + 1 !

E, consequentemente:

e x ≥ 1 + x + · · · + x k k ! + x k + 1 k + 1 ! para x ≥ 0

Assim, para x ≥ 0 , e x ≥ 1 + x + x 2 2 ! +   · · · + x n n ! para todo positivo n , pela indução matemática.

Resposta

Demonstração nos Passos.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja f (x) = x + e^x e seja g a inversa de f . Calcule g^' (1) e g^(' ') (1) .
Verifique que.(d)/(d x) [x arctg x - (1)/(2) ln (1 + x^2)] = arctg x
Determine a derivada.f (x) = (e^(- x) arctg e^x)/(tg x)
Seja f x = x + x 3 .Mostre que f admite função inversa g Expresse g ' x em termos de g x Calcule g ' 0
Seja f x = x + ln ⁡ x , x0 .Mostre que f admite função inversa g , que g é derivável e que g ' x = g x 1 + g x Esboce os gráficos de f e de g Calcule g 1 , g ' 1 e g ' ' 1