Seja , .
- Mostre que admite função inversa , que é derivável e que
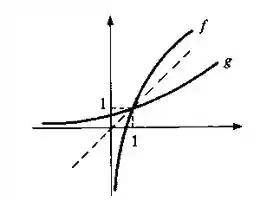
- Esboce os gráficos de e de
- Calcule , e
Passo 1
- Vamos calcular , vamos ver as regras que vamos precisar para calcular as derivadas, vamos usar a regra da função logarítmica natural e do polinômio, além da regra da cadeia:
- Temos que os gráficos de e é da seguinte maneira:
- Vamos calcular :
Assim:
Temos que para todo , logo ela é crescente, assim é uma bijeção de em , então podemos ter a inversa :
Passo 2
Passo 3
Temos que achar quem é , vamos a partir da inversa, como temos que:
Pronto, é só substituir:
Passo 2
Agora vamos achar , para isso temos que achar , aqui vamos usar mais uma regra, a da divisão:
Agora é só aplicar o valor:
Resposta
b) 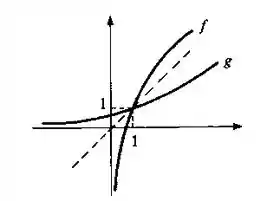
c) , e