Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.2 - Ex. 21
Mostre que a equação tem no máximo uma raiz no intervalo .
Passo 1
Fala aí. Tudo belezinha com você?
Bom, essa questão da pra gente a equação
E pede pra gente mostrar que ela tem no máximo uma raiz no intervalo .
E precisamos encontrar o valor do coeficiente que satisfaça a essa condição.
Para isso, iremos utilizar do Teorema do Valor intermediário.
Vem que te mostro tudinho no passo a passo.
Passo 2
Vamos lembrar que o Teorema do Valor Intermediário diz o seguinte:
Seja
uma função contínua no intervalo fechado
e seja um número real entre e
com
ou
Então, existe pelo menos um tal que
E
Vamos aplicar isso a nossa função.
Passo 3
Seja
dado no intervalo .
O domínio da função é , então é contínua em .
Se tem uma raiz, então para algum .
Assim,
E podemos reescrever como:
definindo
e
Agora vamos desenhar os gráficos dessas funções. Veja:
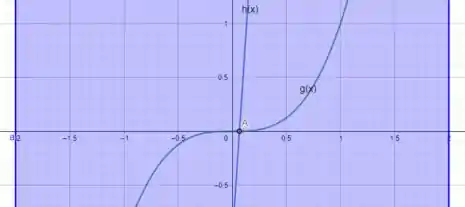
Vemos que os dois possuem exatamente um ponto de interseção, o ponto .
Para o intervalo temos , então .
Passo 4
Agora, calculamos o valor da função nos extremos do intervalo dado. Fazendo:
e
Substituímos e na função
Vamos considerar como uma constante qualquer, por exemplo, .
Assim vemos que
E para
Portanto, aplicando o Teorema do Valor Intermediário, tem uma raiz em .
Resposta
Ver o desenvolvimento.