Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.Revisão - Ex. 34

Mostre que as equações r = 1 + s e n theta e r = s e n theta - 1 tem o mesmo gráfico.

Passo 1

Tá, aqui encontramos algo que vai mecher com seu coração... um cardioide! Ele tem esse formato aí, parecido com um coração.

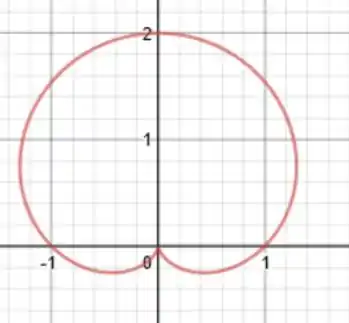
E sem enrolação, vamo provar isso né?!

Passo 2

Vamos sempre lembrar das nossas equações de transformação de polar para cartesianas.

x = r c o s ( theta )

y = r s i n ( theta )

r^2 = x^2 + y^2

Logo, vamos desenvolver a nossa primeira.

r = 1 + s e n theta

sqrt(x^2 + y^2) = 1 + (y)/(r)

sqrt(x^2 + y^2) * sqrt(x^2 + y^2) = r + y

x^2 + y^2 = sqrt(x^2 + y^2) + y

x^2 + y^2 +- sqrt(x^2 + y^2) = y

Legal, essa ta okay. Agora vamos desenvolver a próxima.

r = s e n theta - 1

sqrt(x^2 + y^2) = - 1 + (y)/(r)

sqrt(x^2 + y^2) * sqrt(x^2 + y^2) = - r + y

x^2 + y^2 = - sqrt(x^2 + y^2) + y

x^2 + y^2 +- sqrt(x^2 + y^2) = y

x^2 + y^2 +- sqrt(x^2 + y^2) = y = x^2 + y^2 +- sqrt(x^2 + y^2) = y

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre uma equação polar para a curva representada pela equação cartesiana dada. x + y = 9
Encontre uma equação polar para a curva representada pela equação cartesiana dada. x 2 - y 2 = 1
Encontre uma equação polar para a curva representada pela equação cartesiana dada. x = 3
Encontre a distância entre os pontos com coordenadas polares 1 , π 6 e 3 , 3 π 4 .
Esboce a região do plano que consiste em pontos cujas coordenadas polares satisfazem as condições dadas. - 1 ≤ r ≤ 1 ,π 4 ≤ θ ≤ 3 π 4