Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.2 - Ex. 21

Mostre que função f x = x 4 + 3 x + 1 , tem exatamente uma raíz no intervalo [-2, - 1].

Passo 1

Haja vista que um polinômio de grau n pode apresentar n raízes reais queremos mostrar que no intervalo [-2,-1] a função   f x dada tem exatamente uma raiz.

Passo 2

Começaremos analisando o valor da função nas extremidades do intervalo. Assim, analisando para -2 :

        f - 2 = - 2 4 + 3 * - 2 + 1

f - 2 = 16 + 3 * - 2 + 1

f - 2 = 16 - 6 + 1

f - 2 = 1 1 Para o outro extremo:

f - 1 = - 1 4 + 3 * - 1 + 1

f - 1 = 1 + 3 * - 1 + 1

f - 1 = 1 - 3 + 1

f - 1 = - 1 Como f - 2 > 0   e f - 1 < 0 , o teorema do valor intermediário nos diz que o gráfico de f cruza o eixo x (uma raiz) em algum lugar no intervalo aberto (-2,-1).

Passo 3

Agora, derivaremos a nossa função f x para analisarmos se é possível aplicar o teorema de Rolle. Sendo f x = x 4 + 3 x + 1 ao derivar (utilizando as regras de derivação de polinômio) obtemos:

f ' x =   4 x 3 + 3

Graficamente temos:

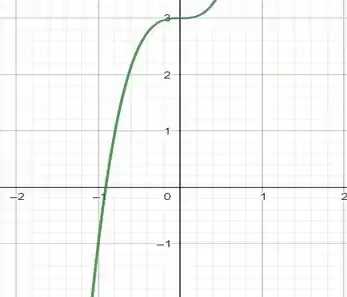
Podemos perceber que no intervalo dado a nossa derivada nunca será 0. Observamos, então, que se houvessem pelo menos 2 pontos a e b para os quais f x = 0 , pelo teorema de Rolle nós deveríamos ter pelo menos um ponto c tal que f ' c = 0 no intervalo dado. Portanto, nesse intervalo f x apresenta exatamente uma raiz.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O Exercício fornece a velocidade v= d s d t e a posição inicial de um corpo que se desloca ao longo de uma reta coordenada. Determine a posição do corpo no instante t para o seguinte caso: v=s e n ( π
Determine todas as funções possíveis com as derivadas dadas: a) y ' =s e n ( 2 t ) b) y ' =c o s ( t 2 ) c) y ' =s e n 2 t + c o s ( t 2 )
Mostre que, em algum momento durante uma viagem de automóvel de 2 horas, o velocímetro marcava o valor equivalente à velocidade média da viagem.
Um atleta percorreu as 26,2 milhas da maratona de Nova York em 2,2 horas. Demonstre que em pelo menos duas ocasiões o maratonista correu a exatas 11m i l h a s / h o r a , supondo que as velocidades i
Relatos antigos contam que um trirreme (navio antigo de guerra grego ou romano), com 170 remos, certa vez percorreu uma distância de 184 milhas náuticas em 24 horas. Explique por que em algum momento