1. Mostre que não é injetora em
2. Encontre o maior valor de , tal que é injetora no intervalo

Beleza, mas como descobrir quem são esses caras? Se a gente olhar com calma a gente consegue fatorar um pouco nossa expressão:

Colocando em evidência:

Essa expressão do segundo grau aí dentro também é favorável, olha só:

Então

Olha com calma, tá vendo que para a expressão vai pro mesmo valor?

Ou seja . Então nossa função de fato não é injetora no intervalo .

Podemos chegar nisso também utilizando o fato de que se a função é injetora no intervalo, então ela também é estritamente crescente ou estritamente decrescente nesse intervalo, e para isso dizemos que se:

No intervalo dado, a função é injetiva nesse intervalo.

No nosso caso:

Como no nosso caso pode assumir tanto valores negativos quanto positivos no intervalo , ela não nem estritamente crescente nem estritamente decrescente, então ela não é injetiva nesse intervalo.

(b)

Precisamos achar o maior valor de tal que a nossa seja injetora no intervalo , porém já vimos que para , , então se o intervalo que a gente quer descobrir contiver esses dois valores, a função já não será injetora.

Logo a gente conclui que com certeza , pois se o intervalo vai conter , e a função não vai ser injetiva.

Massss pensa comigo, se

Então ela tem mais ou menos essa cara aqui, ou algo parecido:

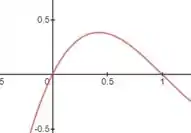
Tá vendo que tem carinhas ali entre que possuem a mesma imagem? Então se pegarmos o não vamos estar garantindo que é injetiva no intervalo.

Precisamos então achar esse ponto extremo da nossa função que está entre

Para achar esses valores de extremo vamos derivar nossa função e igualar ela a zero ():

Então

Como não está entre , então o ponto que nos interessa é

Opaaa então temos que a função é injetora no intervalo ().

Logo