Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.6 - Ex. 55
Mostre que a prova simplificada da regra da cadeia com a exigência adicional (ii) (exercício 54) não é válida para as funções e dadas. Em cada exercício, faça um esboço do gráfico de .
Passo 1
Se você não viu o exercício 54, vai lá dar uma olhadinha e só venha para cá depois de ter entendido!
Para que a regra da cadeia seja válida, devemos ter apenas que e existam, o que é exigido na hipótese (i) da de demonstração no exercício 54. Todavia, para que a demonstração simplificada do exercício 54 seja válida, devemos considerar também a hipótese (ii): para todo num intervalo aberto contendo devemos ter .
Para as funções dadas, devemos verificar que ao menos uma das hipóteses não é satisfeita.
Passo 2
A função é a função maior inteiro, que denota o maior inteiro que seja menor ou igual a . Por exemplo, , enquanto . O gráfico da função é dado a seguir:
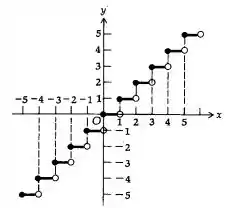
Note que não é contínua para inteiro, de modo que não existe nesses pontos, quebrando a hipótese (i).
Passo 3
Além da hipótese (i) não ser válida para inteiro, para não inteiro, é contínua e existe, porém a hipótese (ii) não é satisfeita: para suficientemente próximo de , temos que ).
Resposta
Demonstração.