Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.1 - Ex. 35
Um cilindro circular reto está inscrito numa esfera de raio dado. Expresse o volume do cilindro em função da altura do cilindro.
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente encontrar uma expressão o volume de um cilindro que está inscrito numa esfera de raio .
Aqui temos um esboço de um cilindro circular reto inscrito numa esfera de raio :
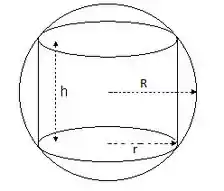
Então, precisamos construir uma expressão de em função da altura . Pra isso, vamos usar a fórmula do volume do cilindro, que é dado pelo produto entre a área da base vezes e a altura, ou seja:
Mas antes precisamos achar o termo em função de para substituir na fórmula do volume, então vamos lá!!
Passo 2
Vamos ver um corte frontal dessa figura, temos que um cilindro tem um triângulo retângulo que é formado pela diagonal, que é igual a duas vezes o raio da esfera, pela sua altura e sua base, mostrada na figura abaixo:
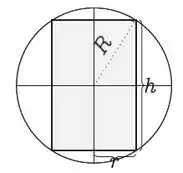
Sendo assim vamos usar Pitágoras nesse triangulo aqui:
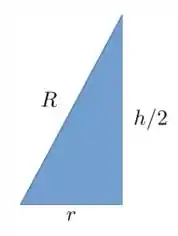
Aplicando Pitágoras:
Passo 3
Vamos destrinchar essa expressão e isolar o raio ao quadrado da base do cilindro:
Agora vamos substituir o na fórmula do volume:
Pronto, substituindo, temos:
E achamos o volume do cilindro em função da altura do cilindro.
Valeu, galera. Até a próxima! 😉