Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.1 - Ex. 28d

Determine o domínio e esboce o gráfico.

g (x) = sqrt(2 - 3 x^2)

Passo 1

Para determinar o domínio devemos ver se a expressão tem alguma limitação, sabemos que raíz não pode envolver número negativo, então vamos pegar a expressão dentro da raíz, fazer ela igual ou maior que zero e resolver:

2 - 3 x^2 >= 0 harr - 3 x^2 >= - 2 harr 3 x^2 <= 2 harr x^2 <= (2)/(3)

Quando temos u^n <= a , se n é par, então - root(n)(a) <= u <= root(n)(a) , então vamos aplicar aqui:

x^2 <= (2)/(3) harr - sqrt((2)/(3)) <= x <= sqrt((2)/(3))

Temos que o domínio é:

D = {x in R | - sqrt((2)/(3)) <= x <= sqrt((2)/(3))}

Passo 2

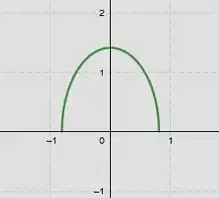
Aqui temos o esboço do gráfico:

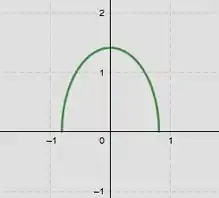
Resposta

D = {x in R | - sqrt((2)/(3)) <= x <= sqrt((2)/(3))}

Esboço do gráfico:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o domínio e a imagem da função e desenhe um esboço de seu gráfico. f x = x 3 + 3 x 2 + x + 3 x + 3
Determine o domínio e a imagem da função e desenhe um esboço de seu gráfico. h x = | x | [ x ]
Determine o domínio e a imagem da função e desenhe um esboço de seu gráfico. f x = x 2 - 3 x - 4
Determine o domínio e a imagem da função e desenhe um esboço de seu gráfico. F x = x 4 + x 3 - 9 x 2 - 3 x + 18 x 2 + x - 6
Determine o domínio e a imagem da função e desenhe um esboço de seu gráfico. f x = x + | x - 1 |