Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 11.6 - Ex. 12
Mostre que a série não pode ser uma série de autofunções para nenhuma função de quadrado integrável.
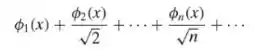
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para analisarmos as deformações verticais de uma barra em suas condições de contorno. Parece muita coisa, mas é tranquilo. Partiu??
Passo 2
Ok, nosso primeiro passo vai ser analisar a equação dada. Para a função, temos que:
Passo 3
Pronto!! Agora é só fazermos umas matemágicas aí pra achar o resultado!!
Resposta
Exercícios de Livros Relacionados
Considere o problema em que α é uma constante dada. Mostre que λ = 0 é um autovalor, se e somente se α = 1.
Suponha que todos os autovalores são reais.Determine a forma das autofunções e a equação satisfeita pelos autovalores não nulos.
Suponha que todos os autovalores são reais.Encontre valores aproximados para λ1 e λ2, os dois autovalores não nulos de menor módulo.
Considere o problema.Mostre que, se φm e φn são autofunções associadas aos autovalores λm e λn, respectivamente, com λm ≠ λn, então
Considere o problema de valores de contorno. Resolva também o problema dado diretamente (sem introduzir uma variável nova).