Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.3 - Ex. 21
O movimento de determinado pêndulo sem amortecimento é descrito pelas equações
Se o pêndulo é colocado em movimento com um deslocamento angular e sem velocidade inicial, então as condições iniciais são
a) Considere e faça o gráfic de em função de . Do gráfico, estime a amplitude e período do movimento resultante do pêndulo.
b) Repita o item (a) para
c) De que modo a amplitude e o período do movimento do pêndulo dependem da posição inicial Desenhe um gráfico que mostra cada uma dessas relações. Você pode dizer alguma coisa sobre o valor limite do período quando
d)Seja e faça o gráfico de em função de . Explique por que esse gráfico difere dos gráficos nos intens (a) e (b). Para que valor de acontece mudança?
Passo 1
a) Para
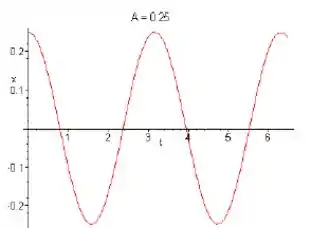
Como o sistema é indiferente e a amplitude é 0,25. O período é estimado em
Passo 2
b)
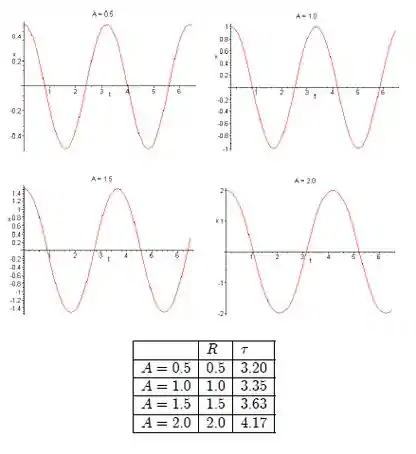
Passo 3
c) Como o sistema é conservativo, a amplitude é igual a amplitude inicial. Por outro lado, o período do pêndulo está em crescimente.
Posição
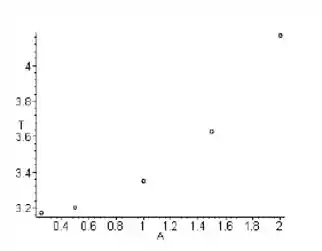
Isso mostra que quando o período de aproxima de , o período do pendulo linear correspondente
Passo 4
d)
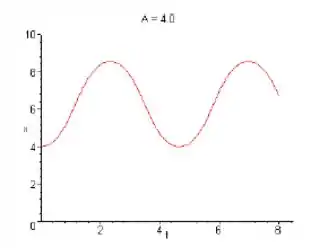
O pendulo parte do descando com inclinação de da vertical. Baseada na conservação de energia, o pêndulo irá balançar além do ponto de equilíbrio debaixo e vem a descansar momentaneamente no A transição entre os dois acontece em , isso é, uma vez que o pendulo é abandonado além da configuração vertical.
Resposta
Ei, a resposta está no passo a passo :)