Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.Exercícios Práticos - Ex. 151a

Movimento do feixe de luz de um farol

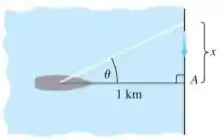
A figura mostra um barco a 1 km de distância da praia, varrendo a costa com um farolete. Este gira a uma taxa constante de .

a. Qual é a velocidade de deslocamento da luz ao longo da costa quando ela alcança o ponto A?

Passo 1

A velocidade de deslocamento da luz que desejamos determinar pode ser representada por e, no momento em que ela alcança o ponto A, o ângulo θ é nulo. Pode-se também criar uma relação entre θ e x:

Passo 2

Derivando a equação gerada em função de t (supondo que x e θ são deriváveis de t) conseguimos encontrar:

Passo 3

Substituindo os dados extraídos do enunciado na última equação encontrada:

Resposta

A velocidade de deslocamento da luz quando ela alcança o ponto A é (o sinal negativo indica que ele desloca para baixo e o sentido positivo é para cima).

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Tanto x quanto y denotam funções de t que estão relacionadas pela equação dada. Use essa equação e a informação sobre a derivada para encontrar a derivada especificada.Equação: x+4 y=3 (a) Dado que d

Em (a) a (d), seja A a área de um círculo de raio r e suponha que r cresça com o tempo t . (a) Faça uma figura do círculo colocando A e r apropriadamente. (b) Escreva uma equação que relacione A e r .

Tanto x quanto y denotam funções de t que estão relacionadas pela equação dada. Use essa equação e a informação sobre a derivada para encontrar a derivada especificada.Equação: 4 x 2+9 y 2=1 (a) Dado

Suponha que z=x 3 y 2 , onde x e y estão variando com o tempo. Em um certo instante, quando x=1 e y=2 , x está decrescendo a uma taxa de 2u n i d a d e s / s e y está crescendo a uma taxa de 3u n i d