Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.Exercícios Práticos - Ex. 89

Determine a altura e o raio do maior cilindro circular reto que pode ser colocado dentro de uma esfera de raio 3 .

Passo 1

Temos a representação gráfica de um cilindro inscrito em uma esfera:

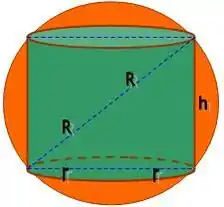
Portanto, por Pitágoras, temos a relação entre r e h:

2 r 2 + h 2 = 2 R 2

4 r 2 + h 2 = ( 2 3 ) 2

4 r 2 + h 2 = 12

Passo 2

Para encontrar o maior cilindro possível, devemos maximizar a expressão do volume V do cilindro.

V = A b . h

V = π r 2 . h

V = π 12 - h 2 4 . h

V = π 4 . 12 h - h 3

Passo 3

A fim de maximizar a expressão do volume, vamos derivar e igualar a zero:

V ' = π 4 . 12 - 3 h 2 = 0

3 h 2 = 12

h = 2

A partir da relação entre h e r (Passo 1), podemos encontrar o valor de r:

4 r 2 + h 2 = 12

4 r 2 + 4 = 12

4 r 2 = 8

r = 2

Resposta

h = 2

r = 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre as dimensões de um retângulo com área de 1000m 2 cujo perímetro seja o menor possível.
Um container para estocagem retangular com uma tampa aberta deve ter um volume de 10m 3 . O Comprimento da base é o dobro da largura. O material para a base custa $ 10 por metro quadrado. O material p
Uma caixa com uma base quadrada e sem tampa tem um volume de 32000c m 3 . Encontre as dimensões da caixa que minimizam a quantidade de material usado.
Um fazendeiro quer cercar uma área de 15000m 2 em um campo retangular e então dividí-lo ao meio com uma cerca paralela a um dos lados do retângulo. Como fazer isso de forma a minimizar o custo da cerc
Uma janela normanda tem a forma de um retângulo tendo em cima um semicírculo. (O diâmetro do semicírculo é igual à largura do retângulo). Se o perímetro da janela for 30p é s é , encontre as dimensões