Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.1 - Ex. 72
Em quais números a seguinte função é derivável?
Dê uma fórmula para e esboce os gráficos de .
Passo 1
Opa, vamos fazer essa questão! O enunciado nos dá:
E pergunta em quais pontos é diferenciável! Percebe que é uma função dividida em partes e dentro de todas elas temos polinômios que sozinhos seriam contínuos pra todo . O problema é na hora de “colar” um polinômio no outro!
Então são esses pontos que vamos investigar, e . Para isso a gente vai calcular a derivada de nesses pontos usando a definição de derivada:
Só que aqui vamos aproximar de zero pela direita e pela esquerda. Se os limites laterais forem iguais, então a nossa função é derivável nesses pontos caso contrário ela não é!
Bora colocar a mão na massa!
Passo 2
Bora começar com , a esquerda temos:
Vamos calcular as derivadas pela definição:
Agora temos pela direita:
Portanto:
Portanto:
Os valores coincidiram, então a função é derivável em .
Passo 3
Vamos ver agora pra . Pela esquerda temos:
Assim:
Pela direita de temos:
Portanto:
Os valores deram diferentes, então a função não é derivável em , então a função é derivável para todos os valores, exceto o .
Passo 4
Temos que:
Agora é só esboçar os gráficos:
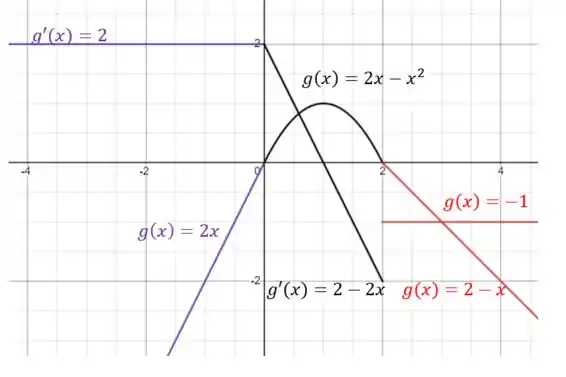
Resposta
A função é derivável para todos os valores, exceto o .