Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 9.3 - Ex. 28

(a) Use um sistema de computação algébrica para desenhar um campo de direção para a equação diferencial. Imprima e use-o para esboçar algumas curvas de solução sem resolver a

equação diferencial.

(b) Resolva a equação diferencial.

(c) Use o SCA para desenhar as soluções obtidas na parte (b). Compare com as curvas da parte (a).

y ' = x y

Passo 1

a) Para saber a inclinação de y ' = x y , podemos criar uma tabela supondo alguns valores de x , y e assim construir o campo de direções.

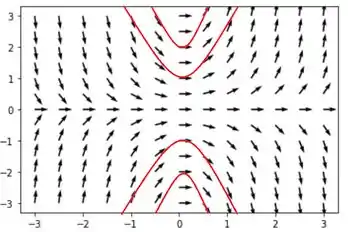
Passo 2

b) Sabemos que y ' = d y / d x , então para encontrarmos a solução da equação diferencial podemos deixar todos os termos que depende de y de um lado da equação e todos os termos que dependem de x do outro lado da equação.

d y d x = x y

d y y = x   d x

Estando seperadas as variáveis, podemos integrar ambos os lados. Sendo esta uma integral indefinida.

∫ d y y = ∫ x   d x

ln ⁡ | y | = x 2 2 + C

Aplicando exponencial em ambos os lados:

y = e x 2 2 + C

Passo 3

c) Plotando o campo de direção encontrado a partir da solução algébrica da equação diferencial e utilizando os mesmos pontos das curvas do intem a), verificamos que ambos são exatamente iguais.

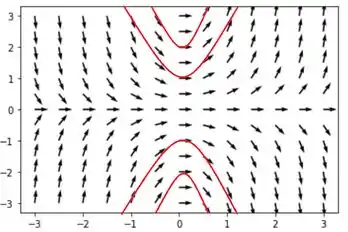
Resposta

b)   y = e x 2 2 + C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esgotamento de petróleo. Suponha que a quantidade de petróleo bombeada de um dos poços do canyon em Whittier, na Califórnia, tenha diminuído a uma taxa contínua de 10 % ao ano.Quando a produção do poç
Esfriamento de sopa. Suponha que, após 10 minutos em uma sala cuja temperatura seja 20 ° C , a temperatura de uma tigela com sopa tenha passado de 90 ° C para 60 ° C . Use a lei do resfriamento de New
Carbono-14. A mais antiga múmia humana congelada conhecida, chamada Otzi, descoberta na geleira Schnalstal, nos Alpes italianos, em 1991 , foi encontrada usando sapatos de palha evestindo um casaco de
A meia-vida do polônio é de 139 dias, mas uma amostra que você recebeu não será mais útil quando 95 % dos núcleos radioativos presentes no dia em que a amostra chegou tiverem se desintegrado. Por quan
Desconto contínuo no preço. Para incentivar os compradores a fazer pedidos de 100 unidades, o departamento de vendas de sua empresa aplica um desconto continuo que toma opreço por unidade uma função p