Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.5 - Ex. 19
A fórmula , onde , expressa a temperatura em graus Celsius como uma função da temperatura em graus Fahrenheit. Encontre uma fórmula para a função inversa e interprete-a. Qual o domínio da função inversa?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente encontrar uma fórmula para a função inversa de:
Pra definir seu domínio e interpretá-la. Sabendo que ela expressa uma temperatura em graus Celsius como uma função da temperatura em graus Fahrenheit, onde .
Pra isso, vamos seguir o passo a passo para encontrar a inversa de uma função:
O domínio de uma função são os valores de para que esteja definida. E pra definir o domínio fazemos o pensamento inverso: pensamos pra quais a função não existe.
Passo 2
Bom, vamos primeiro encontrar a fórmula para a função inversa.
Resumidamente, tudo o que temos que fazer é isolar a variável . Então vamos fazer isso:
Aplicando a distributiva no produto:
Multiplicando os dois lados por :
E isolando , temos:
Pronto, essa é a nossa função inversa! Simples!
E como as variáveis aqui tem um significado muito estabelescido, a gente não pode trocar o nome como as vezes fazemos com e .
Passo 3
Beleza, mas o que ela representa?
A função nos dá a temperatura em graus Fahrenheit, certo? Então, tendo a temperatura em Celsius, podemos utilizar essa fórmula para a transformação da unidade de temperatura.
Enquanto a função inicial converte de Fahrenheit pra Celsius, sua inversa converte de Celsius pra Fahrenheit.
Passo 4
Bom, sobre o domínio, temos que lembrar que, na função inversa, o domínio de f se torna a imagem e a imagem se torna o domínio. Repare nesse exemplo:
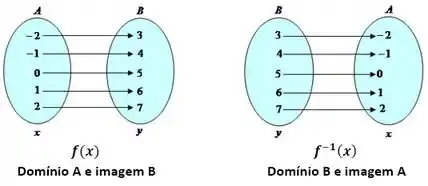
Vamos então achar a imagem da função , que vai ser justamente o domínio da sua função inversa
Como ela é crescente e “começa” em , ela atinge o seu menor valor nesse ponto. Ela também não é limitada, a sua imagem vai até o infinito.
Vamos, então, calcular para esse valor mínimo:
Assim, a imagem de é . E consequentemente, é o domínio da função inversa .
Valeu, galera! Até a próxima! 😉