Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 4.6 - Ex. 1

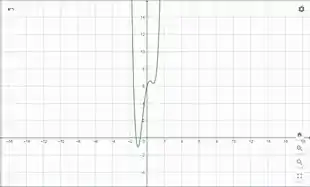
Obtenha gráficos de f que revelem todos os aspectos importantes da curva. Em particular você deve usar os gráficos de f ' e f ' ' para estimar os intervalos de crescimento e decrescimento, valores extremos, intervalos de concavidade e pontos de inflexão.

f x = 4 x 4 - 7 x 2 + 4 x + 6

Passo 1

Bom galera, nesse exercício queremos tirar conclusões e estimar propriedades importantes das funções com base em um gráfico previamente feito. As principais propriedades que queremos estimar são os intervalos de crescimento e decrescimento, valores extremos, intervalos de concavidade e pontos de inflexão. Para isso, iremos primeiramente derivar nossa função duas vezes e com base na análise do gráfico da primeira e da segunda derivada podemos concluir e estimar a respeito da função.

Passo 2

Bom galera, primeiramente iremos encontrar a primeira e a segunda derivada da nossa função para assim fazer o gráfico da função e das suas derivadas. Isso é importante pois ao analisar o gráfico da primeira derivada podemos tirar informações a respeito dos valores de máximo e mínimo local e também podemos estimar os intervalos de crescimento e decrescimento. Ao analisar o gráfico da segunda derivada podemos estimar o intervalo de concavidade e os pontos de inflexão. Derivando f ( x ) , temos

f ' x = 16 x 3 - 14 x + 4

Derivando f ' ( x ) , temos

f ' ' x = f ' x = 48 x 2 - 14

Passo 3

Podemos então gerar os seguintes gráficos

f ( x )

f ' ( x )

f ' ' ( x )

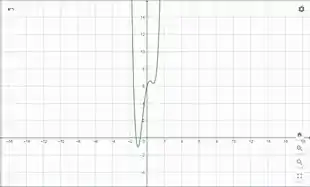
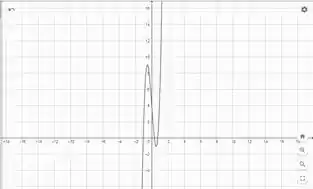
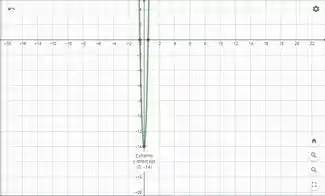
Com base no gráfico de f ' ( x ) , podemos encontrar o intervalo de decrescimento e crescimento. Para isso, devemos ver onde o gráfico de f ' ( x ) é menor que zero. Assim, o intervalo de decrescimento é ( 9.04 ,   - 1.04 ) e o intervalo de crescimento é ( - ∞ ,     9.04 ) e ( - 1.04 ,   ∞ ) . Podemos ver ao olhar pro gráfico também os valores de máximo e mínimo, que estão em ( 0.54 ,   - 1.04 ) para o valor de mínimo e em ( - 0.54 ,   9.04 ) para o valor de máximo.

Com base no gráfico de f ' ' ( x ) , podemos estimar os intervalos de concavidade. Para isso, devemos ver onde o gráfico de f ' ' ( x ) é maior que zero, que é onde a concavidade é para cima. Assim, a nossa função possui concavidade para cima em [ 0.54 ,   ∞ ] e concavidade para baixo em [ - ∞ ,   0.54 ] . Podemos ver também o ponto de inflexão, que é ( 0.54 ,   - 1.04 ) .

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre as assíntotas verticais e horizontais.Encontre os intervalos nos quais a função é crescente ou decrescente.Encontre os valores máximos e mínimos locais.Encontre os intervalos de concavidade e
Encontre as assíntotas verticais e horizontais.Encontre os intervalos nos quais a função é crescente ou decrescente.Encontre os valores máximos e mínimos locais.Encontre os intervalos de concavidade e
O gráfico (do Departamento de Energia dos EUA) mostra como a velocidade do carro afeta o rendimento do combustível. O rendimento do combustível F é medido em milhas por galão e a velocidade v é medida
Faça o gráfico da função usando quantas visualizações retangulares você precisar para descrever a verdadeira natureza da função. f x = e x + ln ⁡ | x - 4 |
Faça o gráfico da função usando quantas visualizações retangulares você precisar para descrever a verdadeira natureza da função. f x = 1 - cos ⁡ x 4 x 8