Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.3 - Ex. 69
Mostre que para . [Sugestão: Mostre que é crescente em .]
Passo 1
Antes de começarmos a questão, vamos fazer uma correção no enunciado. Onde ele diz na verdade é .
Dessa forma, temos que provar que no intervalo .
E temos a sugestão de fazer isso mostrando que é uma função crescente no mesmo intervalo
Inicialmente, nada melhor do que seguir a sugestão que ele nos dá. Ele nos disse para mostrar que é crescente. Para isso, vamos analisar .
Derivando,
Lá da trigonometria a gente sabe o seguinte:
Dividindo os dois lados por para aparecer a
Logo,
Então nossa derivada fica:
Passo 2
Como é sempre positivo no intervalo :
Assim, provamos que nossa função é crescente.
Agora podemos encontrar o valor da nossa função no menor valor do intervalo.
Como ela é uma função crescente no intervalo, certamente ela vai ser maior que esse valor no intervalo.
Dessa forma, vimos que
É uma função que é crescente no intervalo
A função no menor valor do intervalo vale:
E como a função é crescente no intervalo, certamente ela será maior que esse valor dentro do intervalo, portanto:
Dessa forma, provamos que:
No intervalo .
Agora, basta jogar o pro outro lado e então temos:
No intervalo .
Antes de terminar, podemos até esboçar o gráfico de para ver que o que fizemos faz sentido. Olha só:
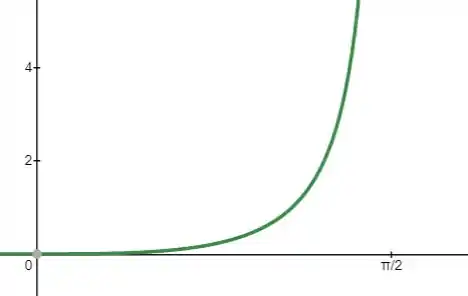
Percebe que essa função é crescente, e como ela começa no , ela certamente é maior do que zero, afinal ela só cresce a partir dali.
Viu que nossa raciocínio tá certo? então tá provado! 😉
Resposta
Desenvolvimento nos Passos.