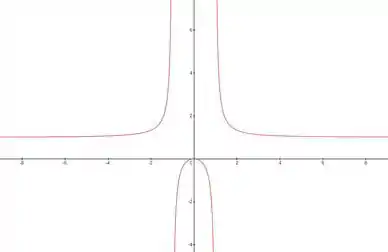
- Encontre as assíntotas vertical e horizontal.
- Encontre os intervalos nos quais a função é crescente ou decrescente.
- Encontre os valores de máximo e mínimo locais
- Encontre os intervalos de concavidade e os pontos de inflexão.
- Use as informações das partes (a)-(d) para esboçar o gráfico de
Passo 1
Fala aí, tudo belezinha com você?
Bom, essa questão dá pra gente a função
E teremos que dizer algumas coisas sobre ela.
No item (a) teremos que encontrar as assíntotas vertical e horizontal, e para isso temos que lembrar do que diz a teoria sobre as assíntotas:
Uma assíntota horizontal é uma reta horizontal de onde a função se aproxima quando tende para . Para encontrarmos essa reta
Já para acharmos as assíntotas verticais, basta acharmos os pontos tais que:
No item (b), precisamos encontrar os intervalos nos quais a função é crescente ou decrescente.
Para saber isso podemos usar as informações dadas pela derivada da função, pois ela representa a inclinação da reta tangente ao gráfico da função. Assim, se
Significa que a função é crescente, já que a reta tangente tem derivada positiva. E se
A função é decrescente, já que a derivada é negativa.
No item (c), queremos encontrar os valores de máximo e mínimo locais.
Para isso também usamos a ideia dada pela inclinação da reta tangente. Ou seja, a derivada. Assim:
Teremos um ponto de máximo ou mínimo da função, já que a inclinação da reta tangente será nula.
No item (d) vamos encontrar os intervalos de concavidade e os pontos de inflexão.
E aqui faremos uso da derivada segunda. Sabendo que se:
Nossa curva terá concavidade para baixo.
E se
E nossa curva terá concavidade para cima.
E finalmente, no item (e) vamos usar as informações das partes (a)-(d) para esboçar o gráfico de .
Agora que já sabemos o que fazer em cada item, vem comigo que te mostro como vai ficar tudo isso.
Passo 2
Vamos começar com o item (a). Ele nos pede para achar as assíntotas vertical e horizontal, mas antes de cair pra dentro vamos analisar o domínio da nossa função.
Repare que a única restrição que temos é que o denominador deve ser diferente de . Assim,
Resolvendo:
Então o domínio será . Agora vamos ver como ficam as assíntotas.
Assíntota vertical:
Para acharmos as assíntotas verticais, basta acharmos os pontos tais que:
Repare que na nossa função isso só ocorre quando o denominador fica igual a . Logo,
Isso quer dizer que as assíntotas verticais são:
e
Assíntotas horizontal:
Se nossa função possuir assíntotas horizontais, basta vermos qual valor do limite quando . olha só:
Como quando o termo fica bem maior que o podemos desprezar o .
Logo, a reta será uma assíntota horizontal.
Passo 3
b) Para acharmos os intervalos nos quais a função é crescente ou decrescente. Vamos analisar o sinal da primeira derivada.
Para fazer essa derivada, podemos usar a regra do quociente, já que a função é formada por uma divisão de outras duas funções. Sendo assim, vamos pensar nela como sendo:
Onde
Com
E
Com
Assim sua derivada será:
Derivando,
Isto é,
Para :
Logo,
Então nossa função será crescente no intervalo .
Para :
Assim,
Então nossa função será decrescente no intervalo .
Passo 4
Para acharmos os pontos de máximo e mínimo, basta fazermos . Então vamos lá!
Como já achamos :
Portanto,
Para sabermos se esse é um ponto de máximo ou mínimo, bastas analisarmos o que achamos no Passo 1. Como para nossa função é decrescente e para nossa função é crescente isso significa que em temos um ponto de mínimo.
Assim, o ponto será um ponto de mínimo.
Passo 5
Agora temos que achar os intervalos de concavidade e os pontos de inflexão. Para isso, vamos achar
Derivando,
Assim,
Para :
Como e é sempre positivo:
Logo,
Assim, nossa curva terá concavidade para baixo no intervalo acima.
Para :
Fazendo a mesma simplificação anterior:
Isto é,
E nossa curva terá concavidade para cima no intervalo acima. Por último, ele nos pede para achar os pontos de inflexão. Logo,
Assim,
Repare que a equação acima não tem solução, porque o termo é sempre positivo. Então, não haverá nenhum ponto de inflexão.
Passo 6
Pra finalizar, vamos esboçar um gráfico. Olha só:

Assim, nosso gráfico será:
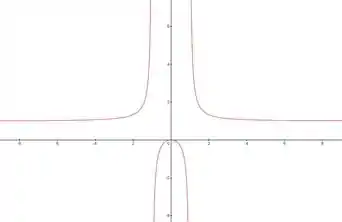
Resposta
a)
Assíntotas horizontais:
e
Assíntotas verticais:
b)
Decrescente:
Crescente:
c)
Ponto de mínimo:
d)
Côncava para cima:
Côncava para baixo:
e) Gráfico de :