Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.8 - Ex. 60
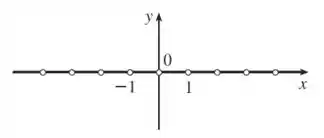
Onde a função maior inteiro não é diferenciável? Encontre uma formula para e esboce seu gráfico.
Passo 1
Eaee, belezinha??? Bom... o enunciado fala sobre a função maior inteiro.
Essa funçãozinha é dada da seguinte forma:
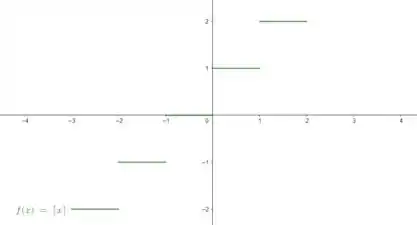
Queremos traçar a derivada e traçar seu gráfico.
Para isso, percebemos que não é contínua em qualquer inteiro
Passo 2
Bom... se ela não é contínua nos números inteiros, então ela não é diferenciável nesses valores!!!
Vamos chamar de os valores que não são inteiros.
Se não é um inteiro, então é constante em um intervalo aberto contendo , então
Assim, , se não é um inteiro.
Esboçando o gráfico, ficamos com a derivada sendo zero em tooodos os números que não são inteiros ().
Por outro lado, não existe derivada nos números inteiros (por isso marcamos uma bolinha branca).
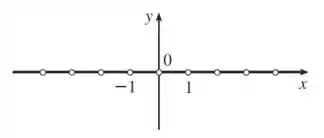
Resposta
A função não é diferenciável nos números inteiros
