Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 5.12 - Ex. 7

Duas industrias necessitam de água potável. A figura a seguir esquematiza a posição das indústrias, bem como a posição de um encanamento retilíneo l , já existente. Em que ponto do encanamento deve ser instalado um reservatório de modo que a metragem de cano a ser utilizada seja mínima?

Passo 1

Para começar, podemos fazer uma ilustração e considerar que a distância do ponto até

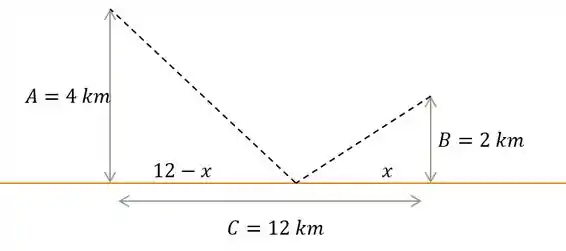
Para acharmos o comprimento l , podemos aplicar o teorema de Pitágoras. Assim,

l x = 4 2 + 12 - x 2 + x 2 + 2 2

Como queremos minimizar a metragem do cano, vamos derivar l em função de x e igualar a zero.

Passo 2

Organizando nossa expressão:

l x = 1 6 + 12 - x 2 1 / 2 + x 2 + 4 1 / 2

Derivando,

l ' x = 1 2 × 1 6 + 12 - x 2 1 2 - 1 × 1 6 + 12 - x 2 ' + 1 2 × x 2 + 4 1 2 - 1 × x 2 + 4 '

Repare que não podemos esquecer da regra da cadeia!

Logo,

l ' x = 1 2 1 6 + 12 - x 2 × 2 ⋅ 1 6 - x ⋅ - 1 + 1 2 x 2 + 4 × 2 x

Simplificando:

l ' x = - 1 6 - x 1 6 + 12 - x 2 + x x 2 + 4

Passo 3

Para achar os pontos críticos, vamos igualar a zero:

- 1 6 - x 1 6 + 12 - x 2 + x x 2 + 4 = 0

Assim,

x x 2 + 4 = 1 6 - x 1 6 + 12 - x 2

Isto é,

x 1 6 + 12 - x 2 = 12 - x x 2 + 4

Elevando ao quadrado em ambos os lados:

x 2 1 6 + 12 - x 2 = 12 - x 2 x 2 + 4

Fazendo a distributiva:

1 6 x 2 + x 2 12 - x 2 2 = x 2 12 - x 2 2 + 4 12 - x 2

Cortando o termo x 2 12 - x 2 2 :

1 6 x 2 = 4 12 - x 2

Abrindo esse termo ao quadrado e simplificando:

4 x 2 = 144 - 24 x + x 2

Isto é,

x 2 + 8 x - 48 = 0

Passo 4

Pra finalizar, vamos resolvendo a equação do segundo grau:

x = - 8 ± 8 2 - 4 × 1 × - 48 2

Como x > 0 :

x = - 8 + 16 2

Agora é só simplificar e correr pro abraço!

x = 8   k m

Resposta

O encanamento deve ser instalado a 8   k m com relação a perpendicular passando por B

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache o valor máximo absoluto e o valor mínimo absoluto da função dada no intervalo indicado pelo método usado nos exemplos 3 e 4 dessa seção. Faça um esboço do gráfico da função no intervalo. f x = x
Ache os extremos absolutos da função dada no intervalo indicado, se existirem, e determine os valores de x nos quais ocorrem os extremos absolutos. Faça um esboço do gráfico da função no intervalo. f
Ache os extremos absolutos da função dada no intervalo indicado, se existirem, e determine os valores de x nos quais ocorrem os extremos absolutos. Faça um esboço do gráfico da função no intervalo. g
Ache os extremos absolutos da função dada no intervalo indicado, se existirem, e determine os valores de x nos quais ocorrem os extremos absolutos. Faça um esboço do gráfico da função no intervalo. g
Ache os extremos absolutos da função dada no intervalo indicado, se existirem, e determine os valores de x nos quais ocorrem os extremos absolutos. Faça um esboço do gráfico da função no intervalo. h