Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.5 - Ex. 49
Em uma órbita lunar o ponto mais próximo da superfície da Lua é chamado perilúnio e o ponto mais distante da superfície da Lua é denominado apolúnio. A nave espacial Apollo II foi colocada em uma órbita lunar elíptica com altitude de perilúnio de e altitude de apolúnio de (acima da Lua). Encontre uma equação dessa elipse se o raio da Lua for e o centro da Lua estiver um dos focos.
Passo 1
Nessa questão, de forma resumida o que nós precisamos fazer é encontrar a equação de uma elipse.
A diferença dessa para outras questões que já fizemos nesse capítulo é que aqui o autor conta uma historinha, dando nomes diferentes para os elementos que temos em uma elipse.
Para entender o que a questão está dizendo, é uma ideia tentar ilustrar isso:
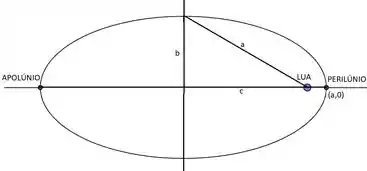
Na nossa figura, vemos que o ponto da elipse mais próximo de um foco é o vértice mais próximo (que é uma distância a partir dele), enquanto o ponto mais distante é o outro vértice (a uma distância de ).
Podemos ver como essa situação se relaciona com a forma de uma elipse ‘comum’ com a figura abaixo:
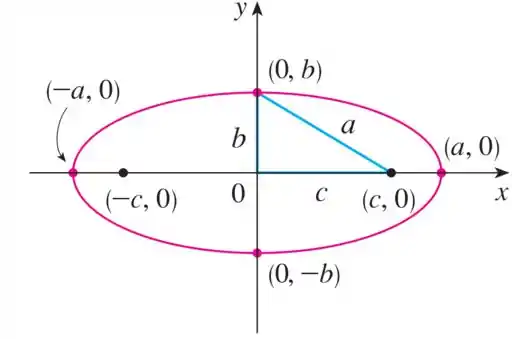
É com essas informações em mãos e comparando com o que normalmente fazemos em relação a descobrir uma equação para uma elipse que iremos resolver essa atividade.
Passo 2
Então, para essa órbita lunar,
E
Da relação entre :
A equação de uma elipse é ora, nós já temos esses valores, só precisamos substituí-los!