Os ornitologistas determinaram que algumas espécies de pássaros tendem a evitar voos sobre largas extensões de água durante o dia. Acredita-se que é necessária mais energia para voar sobre a água que a terra, pois o ar em geral sobe sobre a terra e desce sobre a água durante o dia. Um pássaro com essas tendências é solto de uma ilha que está a do ponto mais próximo sobre uma praia reta, voa para um ponto na praia e então voa ao longo da praia para a área , seu ninho. Suponha que o pássaro instintivamente escolha um caminho que vai minimizar seu gasto de energia. Os pontos edistam um do outro.
(a) Em geral, se é preciso 1,4 vezes mais energia para voar sobre a água do que sobre a terra, para que ponto o pássaro precisa voar para minimizar a energia total gasta no retorno ao ninho?
(b) Sejam e a energia (em joules) por quilômetro voado sobre a água e sobre a terra, respectivamente. Qual o significado, em termos do voo do pássaro, de grandes valores da razão ? O que significaria um valor pequeno? Determine a razão correspondente ao mínimo dispêndio de energia.
(c) Qual deveria ser o valor de a fim de que o pássaro voasse diretamente para seu ninho ? Qual deveria ser o valor de para o pássaro voar para e então seguir ao longo da praia para ?
(d) Se os ornitologistas observarem que pássaros de certa espécie atingem a praia em um ponto a de, quantas vezes mais energia será despendida pelo pássaro para voar sobre a água que sobre a terra?
Passo 1
Fala aí, tudo bem com você?
Bom, esse exercício fala para gente que para um pássaro o gasto de energia para voar sobre o mar é maior que sobre a terra firme.
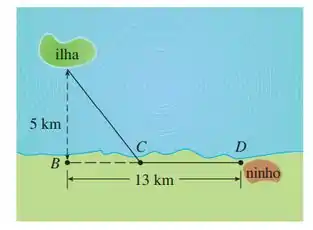
E diz, também, que um pássaro é solto de uma ilha que está a do ponto mais próximo sobre uma praia reta, voa para um ponto na praia e então voa ao longo da praia para a área , seu ninho. Supondo que o pássaro instintivamente escolha um caminho que vai minimizar seu gasto de energia. E sabendo que os pontos edistam um do outro.
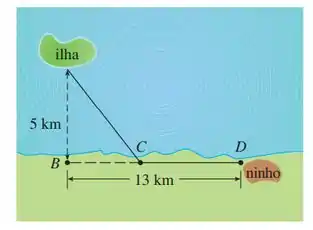
Sobre essa situação, teremos que responder a alguns itens.
No item (a) teremos que dizer onde ficará o ponto que pássaro deve voar pra minimizar o gasto de energia total, considerando que é preciso 1,4 vezes mais energia para voar sobre a água do que sobre a terra.
No item (b) devemos considerar e a energia (em joules) por quilômetro voado sobre a água e sobre a terra, respectivamente, e determinar a razão e dizer o que significar ter essa razão como valores altos e com valores baixos para o voo do pássaro.
No item (c) devemos dizer qual deveria ser o valor de a fim de que o pássaro voasse diretamente para seu ninho , e qual deveria ser o valor de para o pássaro voar para e então seguir ao longo da praia para .
E finalmente no item (d) devemos considerar que os ornitologistas observam que pássaros de certa espécie atingem a praia em um ponto a de, e dizer quantas vezes mais energia será despendida pelo pássaro para voar sobre a água que sobre a terra.
E para responder a todos esses itens devemos encontrar uma relação matemática que descreva o voo desse pássaro de acordo com o trajeto escolhido para assim minimizar o seu gasto de energia e responder a todos esses itens.
Vamos fazer isso juntinhos no passo a passo. Vem comigo.
Passo 2
Podemos começar modelando o voo do pássaro.
Esboçando o desenho e aplicando o teorema de Pitágoras, ficamos com:
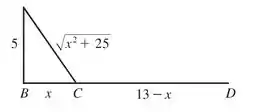
Show, agora com essa relação matemática de cada etapa do voo, vamos resolver cada um dos itens.
Passo 3
No item (a) desejamos minimizar a energia gasta no voo.
Considerando como a energia por quilômetro sobre a terra, então a energia por quilômetro sobre a água será , então a fórmula da energia total é:
Nesse caso,
Como queremos a menor energia gasta, podemos minimizar essa expressão de energia fazendo a derivada e igualando a zero. Assim:
Minimizando através da derivação por regra da cadeia, teremos:
Agora igualando a zero, ficamos com:
E agora teremos que resolver essa equação.
Assim, a raiz será:
Testando os valores extremos de :
Então, para minimizar energia deve voar a um ponto à cerca de de .
Passo 4
Agora vamos ao item (b).
Devemos pensar o seguinte:
Se é grande, o pássaro deve voar para um ponto que é mais próximo de que de para minimizar a energia usada voando sobre a água.
Se é pequeno, o pássaro deve voar para um ponto que é mais próximo de que de para minimizar a distância do voo.
Assim,
Minimizando :
Seguindo o mesmo argumento de (a), essa relação dará o gasto mínimo de energia se a ave se dirigir ao ponto à cerca de de .
Passo 5
Agora no item (c) vamos ver o que acontece quando o pássaro voa diretamente para .
Para isso, faremos , então usando a resposta de (b) temos:
Não há valor de para o qual o pássaro deveria voar diretamente para , mas se fizermos
Se o ponto que a energia é mínima é perto de , então é grande, porque a energia gasta voando sobre a água estará tendendo a zero.
Passo 6
Agora em (d), assumindo que os pássaros com certeza escolham o caminho que minimize o gasto de energia, podemos usar a equação da parte a para derivar em função de , com e :
E prontinho. Temos tudo que foi pedido.
Resposta
a) O pássaro deve voar a um ponto à cerca de de .
b) Se é grande, o pássaro deve voar para um ponto que é mais próximo de que de para minimizar a energia usada voando sobre a água.
Se é pequeno, o pássaro deve voar para um ponto que é mais próximo de que de para minimizar a distância do voo.
c) Para voar diretamente para
Não há valor de para o qual o pássaro deveria voar diretamente para
d)