Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.2 - Ex. 10
Um paciente recebe uma injeção de 150 mg de uma droga a cada 4 horas. O gráfico mostra a quantidade da droga na corrente sanguínea após horas. (Posteriormente poderemos calcular a dosagem e intervalos de tempo que garantam que a concentração da droga não atinja níveis perigosos.) Encontre
E
E explique significado desses limites laterais
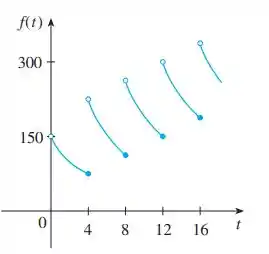
Passo 1
Eaee, belezinha?? Bom... o enunciado nos dá o seguinte gráfico que descreve a quantidade da droga na corrente sanguínea após horas:
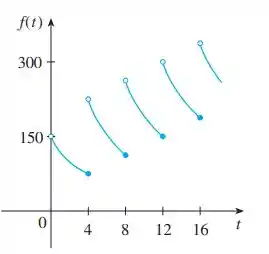
Com isso, queremos encontrar os seguinte limites laterais (e explicar eles):
E
Bom... Toda a situação dada é para que possamos analisar o limite da função a medida que nos aproximamos de pela esquerda e pela direita.
Para encontrarmos o limite lateral é interessante analisar os valores para os quais a função se aproxima a depender de que lado nos analisamos.
Se é o limite pela esquerda (quando ) ou o limite pela direita (quando ).
Agora vamos aplicar!! 😉
Passo 2
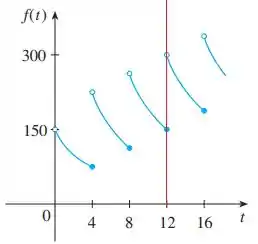
Pelo gráfico, podemos ver que se a gente se aproximar de 12 pela esquerda, a função se aproxima de , ou seja:
E se formos pela direita, vai ser aquele outro trecho, a função se aproxima de :
Isso mostra que ocorre uma mudança abrupta na concentração do remédio no sangue do paciente em .
Passo 3
O limite a esquerda, mostra a concentração do remédio no sangue imediatamente antes da quarta injeção.
Já o limite a direita, mostra a concentração do remédio no sangue logo após a quarta injeção.
Entendeu direitinho?? Responde aee 😉
Resposta
e .
O limite a esquerda, mostra a concentração do remédio no sangue imediatamente antes da quarta injeção. Já o limite a direita, mostra a concentração do remédio no sangue logo após a quarta injeção.