Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.5 - Ex. 60
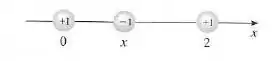
A Lei de Coulomb afirma que a força de atração entre duas partículas carregadas é diretamente proporcional ao produto das cargas e inversamente proporcional ao quadrado da distância entre elas. A figura mostra partículas com carga localizadas nas posições e sobre o eixo das coordenadas, e uma partícula com a carga em uma posição entre elas. Segue da Lei de Coulomb que a força resultante agindo sobre a partícula do meio é
Em que é uma constante positiva. Esboce o gráfico da função força resultante. O que o gráfico mostra sobre a força?
Passo 1
Fala aí, tudo certinho com você?
Bom, esse exercício dá pra gente a seguinte configuração de cargas:
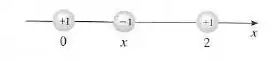
E diz que a força resultante sobre a partícula que está na posição é dada por:
E teremos que esboçar o gráfico de para ver como a força de atração entre as partículas se comporta em função da distância entre elas.
Para isso, iremos utilizar os conceitos desse capítulo para concluirmos sobre o gráfico a respeito do comportamento da partícula.
Então iremos procurar o domínio da função, os pontos de interseções com os eixos, as assíntotas, as regiões onde a força é crescente e decrescente, os pontos de máximos e mínimos e a concavidade.
Vamos ver cada uma dessas características juntinhos no passo a passo. Vem comigo.
Passo 2
Sendo
Domínio. A função dada é definida no intervalo dado de acordo com as características do enunciado.
Interceptações. As interceptações no eixo , acontecem para:
Assim, faremos:
E não há interceptação no eixo pois a função não está definida em .
Vamos ver agora se á simetria.
Para isso, faremos para encontrar qualquer simetria:
Essa expressão não é igual nem a nem a , o que significa que o gráfico não terá simetria.
Passo 3
Agora vamos ver se temos alguma assíntota.
Como o domínio é , pode haver assíntotas verticais em e .
Encontrando os limites unilaterais, faremos:
E
Portanto, essas linhas são assíntotas verticais. Não há assíntotas horizontais, pois o domínio é um intervalo limitado.
Intervalos de aumento e diminuição. Para encontrar esses intervalos, precisamos da primeira derivada:
Nós temos
E resolvendo, ficamos com
Tirando o mmc, teremos:
E resolvendo, ficamos com
Observe que (1) é verdadeiro porque e para todos os no domínio. A conclusão (2) é verdadeira porque a função quadrática é negativa para todos os números reais. Portanto, a função dada está aumentando em todo o domínio.
Passo 4
Extremos locais. Não há extremos locais, pois a função é estritamente crescente.
Concavidade e pontos de inflexão. A segunda derivada é:
Portanto
Da mesma forma,
para , então é côncava para cima para e côncava para baixo para . Além disso,
é um ponto de inflexão.
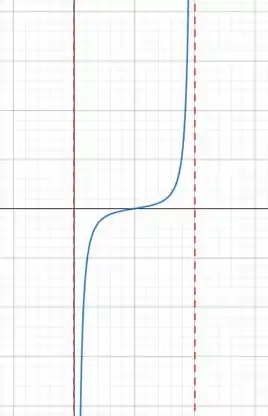
O gráfico:
Resposta
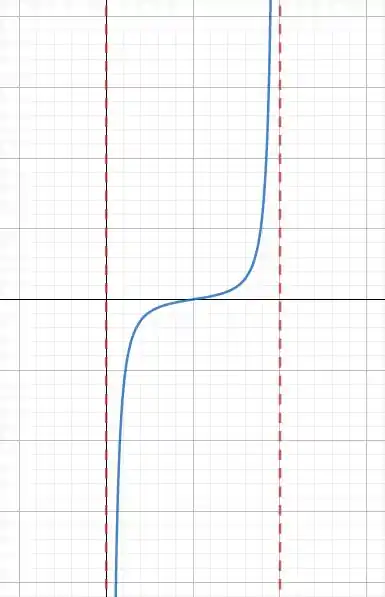
Podemos ver pelo gráfico que em a força atuante é nula. Quando a distância é maior que , a força aumenta com a distância e quando a força é menor que , a força é negativa, então atua no sentido oposto.