49. Uma partícula move-se de acordo com uma lei do movimento , onde está medindo em segundo e , em metros.
(a) Encontre a aceleração no instante e depois de
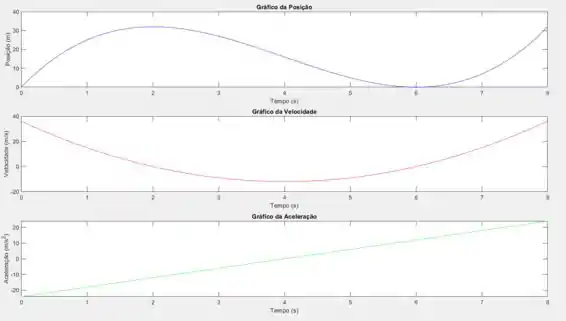
(b) Faça o gráfico das funções posição, velocidade e aceleração para .
(c) Quando a partícula está aumentando a rapidez? E quando está diminuindo?
Passo 1
Aeee galeraaa, bom diiiiaa haha ceis tão bonzinhoo?
(a) Para encontrar a aceleração precisamos derivar duas vezes a função de posição em relação ao tempo , ou seja, .
Derivando uma vez, obtemos a velocidade:
Derivando novamente, obtemos a aceleração:
Para encontrar a aceleração no instante substituímos na expressão
Para segundos:
Portanto, a aceleração após 3 segundos é .
Passo 2
(b) Podemos plotar esse gráfico no geogebra ou em matlab, o exemplo que eu trouxe e do matlab, como mostra o codigo a seguir, e a resposta no gráfico
% Definindo a função posição s(t)
s = @(t) t.^3 - 12*t.^2 + 36*t;
% Definindo a função velocidade v(t)
v = @(t) 3*t.^2 - 24*t + 36;
% Definindo a função aceleração a(t)
a = @(t) 6*t - 24;
% (a) Calculando a aceleração no instante t e depois de 3s
t = 3; % Tempo em segundos
aceleracao_no_instante_t = a(t);
disp(['A aceleração no instante t é ', num2str(aceleracao_no_instante_t), ' m/s^2']);
% (b) Gráfico das funções posição, velocidade e aceleração para 0
t_values = linspace(0, 8, 100); % Valores de tempo
s_values = s(t_values); % Valores de posição
v_values = v(t_values); % Valores de velocidade
a_values = a(t_values); % Valores de aceleração
% Gráfico das funções posição, velocidade e aceleração juntos
figure;
% Gráfico da posição
subplot(3,1,1);
plot(t_values, s_values, 'b');
title('Gráficos de Posição, Velocidade e Aceleração');
xlabel('Tempo (s)');
ylabel('Posição (m)');
hold on;
% Gráfico da velocidade
subplot(3,1,2);
plot(t_values, v_values, 'r');
xlabel('Tempo (s)');
ylabel('Velocidade (m/s)');
hold on;
% Gráfico da aceleração
subplot(3,1,3);
plot(t_values, a_values, 'g');
xlabel('Tempo (s)');
ylabel('Aceleração (m/s^2)');
hold off;
Passo 3
Quando a partícula está acelerando? Quando está freando?
A partícula está acelerando quando e possuem o mesmo sinal. Logo, ela está acelerando no intervalo:
A partícula está freando quando e possuem sinais opostos. Logo, ela está freando nos intervalos:
Poderiamos também ter observado o gráfico do passo anterior!
Resposta
(a)
(b)
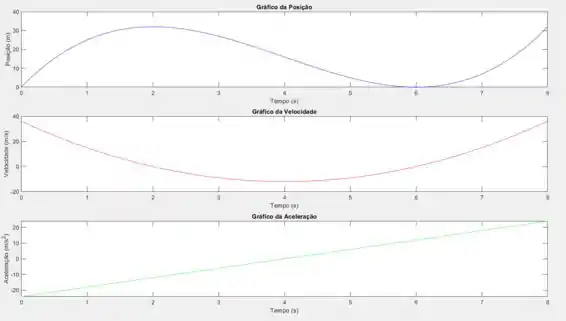
(c)